The Periodic Table Again
See also: The Periodic Table VSI | Memorizing the periodic table | Elements | Elements II
I have just finished reading Eric Scerri’s book “The Periodic Table: Its Story and Significance” (OUP, second edition, 2020). Scerri also wrote the Periodic Table VSI. This post recaps some aspects I found particularly interesting.
1 Simple substances versus basic substances
Scerri draws a sharp distinction between two ideas that are often blurred:
Elements as simple substances. This is the old, laboratory-facing notion. A simple substance is what you can actually isolate in a test tube: oxygen gas, metallic iron, sulfur crystals. It is matter made entirely of atoms of one type, and it has observable chemical properties.
Elements as basic substances. This is the deeper, ontological notion. A basic substance is the underlying atomic species itself (O, Fe, S), defined by nuclear charge (atomic number), regardless of the form in which it appears. You never literally observe a basic substance; you observe its manifestations as compounds or as simple substances.
Scerri argues that chemistry needs both notions but that the basic substance is the more fundamental one. The element is not the gas, metal, or crystal you can isolate. It is the abstract atomic kind that persists through all chemical transformations. Simple substances are just one expression of that deeper entity.
2 The perfect periodic table?
Towards the end of the book, Scerri muses about a perfect periodic table.
…if the elements are presented in the form of a left-step table all triads of elements without exception consists of sets of three elements in which the second and third of them belong to periods of equal lengths. I now believe that this presents a further and admittedly formal argument in favor of the superiority of the left-step periodic table. It is also my belief that this table may provide the long-sought optimal periodic table. (bold added)
Scerri, Eric. The Periodic Table: Its Story and Its Significance (p. 402). Oxford University Press. Kindle Edition.
Figure 1 shows an example of the left-step table from the comprehensive INTERNET Database of Periodic Tables.
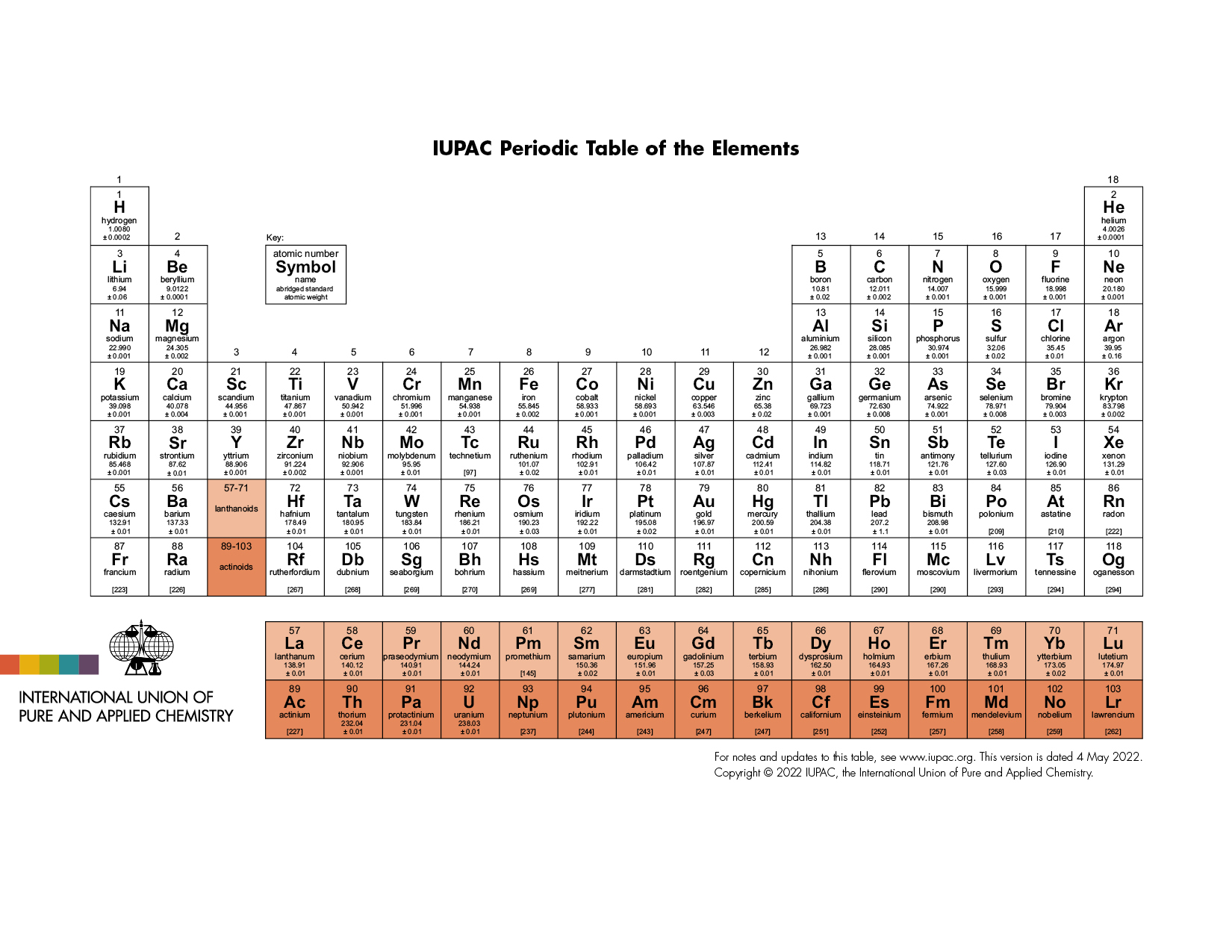
3 The current IUPAC table
Scerri reports that, at present, there is no official recommendation from IUPAC. Figure 2 is the latest version on their website.
They also show an interesting version including isotope information, Figure 3.
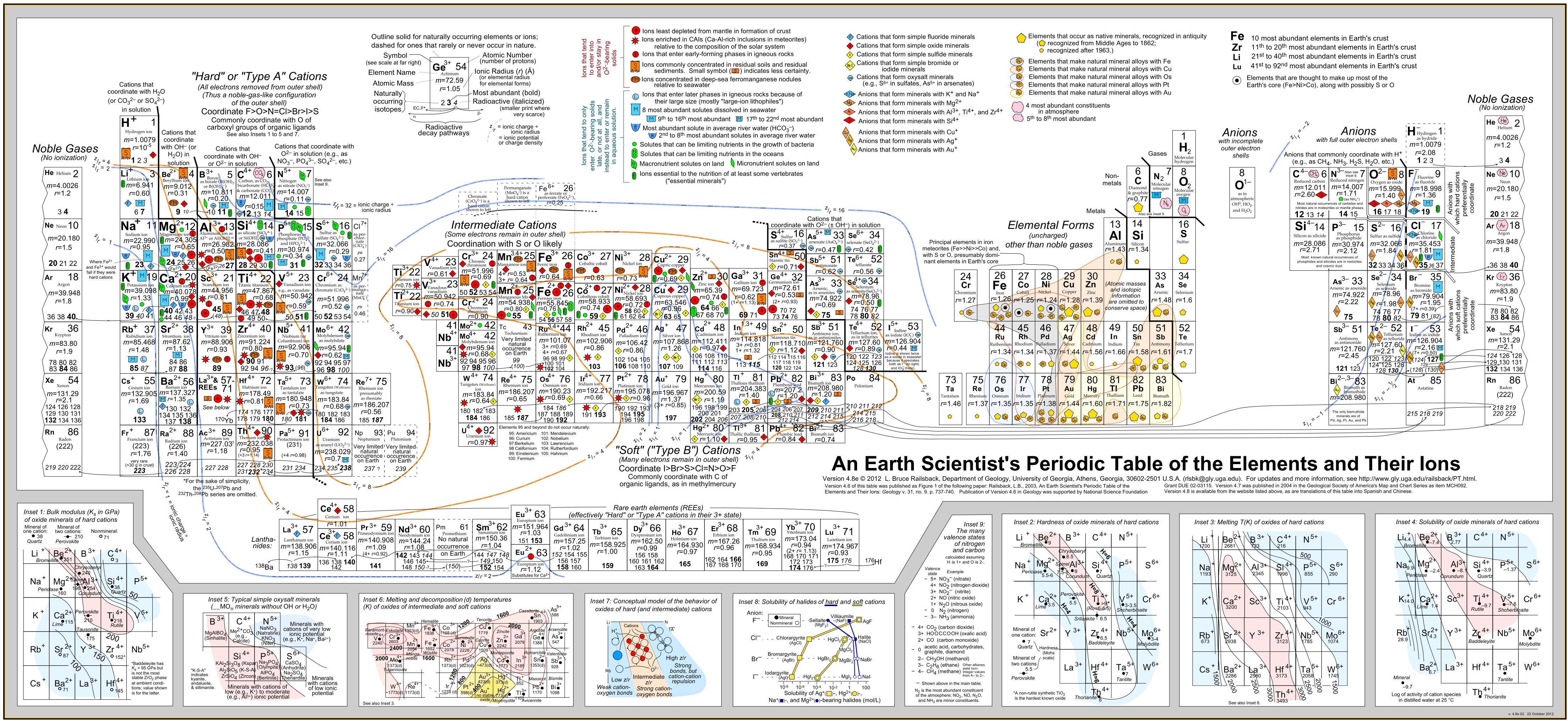
4 An earth scientist’s periodic table
Geologist Bruce Railsback has created “An Earth Scientist’s Periodic Table” of the elements and their ions, Figure 4. It arranges lithophiles (rock-loving, found in oxide minerals or as halides), siderophiles (iron-loving in the core), and chalcophiles (found in the crust with non-metals) into distinct groups. It also tries to group elements into naturally occurring sets, depending on whether they might be concentrated in the mantle, in seawater, or in soil.
Railsback has a fantastic website of geoscience resources.
5 Superatom clusters
The recent discovery of superatom clusters threatens to disturb the peaceful order of the periodic table in a radical manner.28 Some chemical elements present in the form of clusters or “superatoms” can take on the properties of entirely different elements that are completely unrelated in terms of their grouping. Indeed, some cases of a single element can be made to mimic several different elements according to the precise number of atoms present in its cluster. In the 1980s, Thomas Upton at Caltech discovered that a cluster of six aluminum atoms could catalyze the splitting of hydrogen molecules, thus mimicking the behavior of the element ruthenium. (ibid. p. 418.)
6 The end of electrons
At the end of the chapter on super-heavy elements Scerri reports:
In 2017, a paper was published involving a collaboration between scientists in various countries, aimed at exploring element 118 or oganesson, which is currently the heaviest atom ever produced.49 The predictions indicate rather extreme relativistic effects, which show that this atom may not have electrons in shells as is the norm for all previous atoms. The electrons are expected to form a kind of soup. As a result the periodic table will become even more irrelevant when it comes to predicting the properties of the atom than the kinds of relativistic effects that have been known to occur in elements such as gold and lead or dubnium and rutherfordium.
But even more startlingly, the calculations carried out by this team led by New Zealander Peter Schwerdtfeger indicate that at certain even higher atomic numbers there will come a point at which nuclei will not even have any electrons, regardless of whether they occur in shells or otherwise. If this is correct, it would mean the end of chemistry in an even more profound sense since chemical behavior is governed by the electrons in an atom. Finally and even more bizarrely, these predictions indicate that at certain atomic number values atoms accompanied with electrons will begin to appear once again. This implies that the periodic table would have genuine gaps in which there are no atoms, as we generally know them, that are capable of showing chemical behavior. (ibid.pp. 367-368)
7 Electron configurations
7.1 Aufbau principle (Madelung / \(n + \ell\) rule)
The Aufbau (from German: Aufbauprinzip, literally ‘building-up principle’) principle is an approximate guideline for the order in which orbitals are filled when building up the periodic table. It states that orbitals are filled in order of increasing values of \[ n + \ell , \] where
- \(n\) is the principal quantum number,
- \(\ell\) is the orbital angular momentum quantum number (\(0\) for s, \(1\) for p, \(2\) for d, \(3\) for f).
If two orbitals have the same value of \(n + \ell\), the one with the lower \(n\) is filled first.
Example:
- \(4s\): \(n=4\), \(\ell=0\), so \(n+\ell=4\)
- \(3d\): \(n=3\), \(\ell=2\), so \(n+\ell=5\)
Thus \(4s\) fills before \(3d\).
Important: The Aufbau principle is not exact. It works well for most elements, especially at the beginning of each block, but it has well-known exceptions (Cr, Cu, Nb, Mo, Ru, Rh, Pd, Ag, Pt, Au, etc.). It comes from approximate central-field models of atoms and fails when electron–electron interactions reshape the energy ordering.
7.2 Hund’s rule (Hund’s first rule)
Hund’s rule governs how electrons fill degenerate orbitals (orbitals of the same energy within the same subshell).
Statement:
- When electrons occupy orbitals of equal energy (for example, the three \(p\) orbitals or five \(d\) orbitals), they spread out so that each orbital gets one electron before any gets two.
- Moreover, these single electrons have parallel spins (same spin quantum number).
Reason:
- Electrons repel one another.
- Spreading out reduces electron–electron repulsion.
- Parallel spins give a larger total spin and lower the energy via exchange interaction.
Exactness: Hund’s rule follows from fundamental quantum mechanics (electron repulsion + exchange). It is extremely reliable for ground-state electron configurations of neutral atoms and ions.
7.3 Pauli exclusion principle
Pauli’s principle states: \[ \text{No two electrons in an atom can have the same set of four quantum numbers } (n, \ell, m_\ell, m_s). \] Consequences:
- Each orbital, defined by \((n,\ell,m_\ell)\), can hold at most two electrons.
- If two electrons are in the same orbital, they must have opposite spins (\(m_s = +\tfrac{1}{2}\) and \(m_s = -\tfrac{1}{2}\)).
Exactness: The Pauli exclusion principle is a fundamental law of physics that follows from the antisymmetry of fermionic wavefunctions. It has no exceptions.
7.4 Summary of correctness
| Principle | Nature | Correct? | Notes |
|---|---|---|---|
| Aufbau (\(n + \ell\) rule) | Empirical / model-based guideline | Approximate | Many exceptions; still useful for broad patterns. |
| Hund’s rule | Physical rule from exchange + repulsion | Very reliable | Holds for essentially all ground states of atoms. |
| Pauli exclusion | Fundamental fermion principle | Exact | No known exceptions anywhere in physics. |
8 Atomic weight, atomic number, and Moseley’s Method
Henry Moseley discovered that a better ordering principle for the periodic system is atomic number rather than atomic weight. He did this by subjecting samples of many different elements to bombardment with X-radiation. Moseley died in the First World War aged 26, before becoming known. His fame is based on two articles that established that atomic number as the ordering principle for the elements. Moseley states:
We have here a proof that there is in the atom a fundamental quantity, which increases by regular steps as we pass from one element to the next. This quantity can only be the charge on the central positive nucleus, of the existence of which we already have definite proof. (H.G.J. Moseley, Atomic Models and X-Ray Spectra, Nature, 92, 554, 1913.)
Moseley applied this work in settling outstanding questions. Scerri describes how
Georges Urbain, a French chemist known for his work on the isolation of rare earth elements, traveled to Oxford in order to meet Moseley after hearing of his groundbreaking work. As the story goes, Urbain handed Moseley a sample containing a mixture of rare earths and challenged him to identify which elements were present. After a matter of about one hour, Moseley is said to have surprised Urbain by correctly identifying the presence of erbium, thulium, ytterbium, and lutetium in the Frenchman’s sample. The same feat had taken Urbain several months to achieve by chemical means. Urbain then asked Moseley to tell him the relative amounts of the various elements in the sample and was again astonished to receive an answer that coincided almost exactly with his own laborious chemical analysis.
Moseley’s work clearly showed that successive elements in the periodic table have an atomic number greater by one unit. From this fact, Moseley and others could identify which gaps remained to be filled in the periodic system and found that there were a total of seven such cases still waiting to be discovered. Unlike previous lists of gaps, this list was now completely definitive and included the precise atomic numbers of the still elusive elements, which were 43, 61, 72, 75, 85, 87, and 91.32
The clarification that Moseley brought to the periodic table represents one of the finest examples of the reductive power of physics in the field of chemistry. Most lingering problems regarding pair reversals, such as those concerning tellurium and iodine, which had plagued Mendeleev throughout his career, were thereby resolved. Furthermore, Moseley’s work made it easier to deal with the profusion of apparent new “elements” that emerged as a result of research on radioactive phenomena. Two substances could be regarded as being the same element if, and only if, they showed the same value of atomic number, which could be clearly measured by Moseley’s method. (ibid. p. 188, bold added.)
Here are some more details of Moseley’s Method
8.1 Before atomic number (mid-1800s)
The periodic table is first organized by atomic weight (Mendeleev 1869; Meyer 1864–1870). Most patterns fit, but several stubborn anomalies do not: Co–Ni, Te–I, Ar–K, Th–Pa. Chemists regard the ordering by properties is correct, but the masses disagree, and no one knows why.
During the late 1800s the nature of charge also becomes clearer. By the 1890s it is known that the magnitude of positive and negative charge is the same (Stoney, Thomson, others), hinting at a deep structural symmetry.
8.2 Rutherford and the nuclear picture (1911)
Rutherford shows that atoms contain a tiny, massive, positively charged nucleus. The amount of positive charge is not yet measured directly, but it is assumed to be an integer multiple of the elementary charge. However, nobody knows how to determine that integer for each element.
8.3 The idea of atomic number (early 1910s)
Van den Broek (1911–1913) proposes that the integer nuclear charge is the true ordering principle for the periodic table. This is a bold hypothesis but lacks experimental measurement. Scerri recounts how Van den Broek was an amateur scientists.
8.4 Moseley’s breakthrough (1913–1914)
Henry Moseley measures characteristic x-ray frequencies emitted by pure elements when bombarded with high-energy electrons. He focuses on K-series lines, which arise when an inner (1s) electron is knocked out and an outer electron drops into the vacancy. His key observation (1913) is that for each element \[ \nu(K_{\alpha}) \propto (Z-1)^2 . \] Plotting \(\sqrt{\nu}\) against the element’s place in the periodic table gives a strikingly straight line. The offset by \(1\) reflects simple screening: in the 1s shell one electron effectively hides one unit of nuclear charge from the other. Everything looks as though the inner electron sits on a giant hydrogen atom with nuclear charge \(Z-1\).
Quickly:
- The deepest electrons live right next to the nucleus.
- From that close-up view, the atom looks like a giant version of hydrogen with nuclear charge \(Z-1\), \(Z\) from protons and \(-1\) from the other 1s electron.
- When an electron falls into the 1s hole, it emits an x ray whose frequency is basically \((Z-1)^2\) times a fixed constant.
- Moseley measured those frequencies.
- They lined up perfectly with \((Z-1)^2\).
- That proved atomic number \(Z\) is real, measurable, and the correct way to order the periodic table.
8.5 Mathematical sketch
Inner-shell electrons see a nearly bare nucleus. Outer electrons lie far away and contribute almost no screening at such short distances, so the 1s region behaves almost exactly like a hydrogen atom with an effective nuclear charge \[ Z_{\text{eff}} = Z - \sigma, \] where \(\sigma\) is the screening constant. For a 1s vacancy, only the remaining 1s electron lies inside the transition, so \(\sigma \approx 1\).
Hydrogenic energy levels have the form \[ E_n = - R, \frac{Z_{\text{eff}}^2}{n^2}, \] with \(R\) the Rydberg constant. Moseley studies the \(K_{\alpha}\) line, the transition \(n=2 \to n=1\). Using \(Z_{\text{eff}} = Z - 1\), \[ \begin{aligned} h\nu &= E_2 - E_1 \\ &= R (Z-1)^2\left( \frac{1}{1^2} - \frac{1}{2^2} \right) \\ &= \frac{3}{4} R (Z-1)^2. \end{aligned} \] Thus \[ \nu \propto (Z-1)^2, \] which is the empirical relation Moseley uncovers.
8.6 Why this works
The crucial fact is that inner electrons live deep in the Coulomb well of the nucleus. At those distances:
- chemistry is irrelevant
- bonding is irrelevant
- all outer electrons are effectively outside
- the potential is dominated by the nuclear charge
So the 1s electron feels the same physics as the electron in hydrogen, only with a larger nuclear charge. That is why the simple hydrogenic formula survives and why Moseley’s rule is so clean.
8.7 Consequences
- Moseley provides the first direct physical measurement of the atomic number \(Z\).
- Periodic-table anomalies disappear: ordering by \(Z\) aligns perfectly with chemical properties.
- The measured sequence reveals real gaps (then-missing \(Z=43,61,72,75\)).
- The periodic table becomes anchored in nuclear charge, not atomic weight.
Moseley’s work is the experimental turning point that establishes \(Z\) as the fundamental ordering principle of the elements.
8.8 Definitions
| Symbol / term | Meaning (ELI5 version) |
|---|---|
| \(K\) series | The set of x rays produced when an electron falls into the innermost hole in an atom (the 1s shell). Think of it as the atom’s deepest, strongest x-ray shout. |
| \(K_{\alpha}\) line | The specific x ray produced when an electron drops from the second shell (\(n=2\)) down into the 1s hole (\(n=1\)). This is the brightest, easiest-to-measure line in the K series. |
| 1s shell | The very lowest, closest electron orbit around the nucleus. Every atom tries to put up to two electrons there. |
| \(\nu\) | The frequency of the emitted x ray (how many light-wave wiggles per second). Higher \(\nu\) means a more energetic x ray. |
| \(h\) | Planck’s constant. The rule that links energy and frequency by \(E = h \nu\). Kids’ version: the price tag for one light-wave wiggle. |
| \(Z\) | Atomic number: the number of protons in the nucleus. This is the true identity tag of an element. (Not atomic weight!) |
| \(\sigma\) | Screening constant. How much the other inner electron blocks the view of the full nuclear charge. For a 1s hole, \(\sigma \approx 1\) because the remaining 1s electron hides almost exactly one unit of charge. |
| \(Z_{\text{eff}}\) | Effective nuclear charge: \(Z - \sigma\). What the falling electron actually feels. |
| \(R\) | The Rydberg constant. The number that appears when you compute energy levels for a hydrogen atom. |
| \(E_n\) | The energy of the hydrogen-like level with principal quantum number \(n\). Lower \(n\) means closer to the nucleus and more tightly bound. |
| Hydrogenic | Behaving like the electron in a hydrogen atom but with a bigger nucleus. The 1s region of heavy atoms looks almost exactly like this. |
9 Reduction of chemistry to physics
Scerri discusses reduction extensively. He argues that quantum mechanics underpins the structure of chemistry, but it does not fully determine chemical facts in a clean, deductive way. The fundamental equations are known, yet for real atoms and molecules the many-electron Schrödinger equation cannot be solved exactly. Chemists work with approximate models whose success depends on experience, heuristics, and empirical tuning. This is why the periodic table retains its autonomy: physics constrains it, but does not derive it line by line.
Scerri highlights several places where chemistry outstrips straightforward quantum prediction. The Aufbau pattern Section 7.1 is not derivable from first principles and has well-known exceptions (Cr, Cu, Pd, Au), where the predicted electron configuration differs from the experimentally observed one. Moreover, some configurations depend critically on relativistic effects, especially for heavier elements where inner electrons move fast enough that their mass effectively increases. These relativistic shifts help explain why gold is yellow, mercury is liquid, lead loses its 6p electrons readily, and why lanthanide and actinide contractions occur. But the need for these adjustments is typically recognized after the chemical facts are known; you do not predict the anomalies from pure theory alone.
Another example is the ordering of orbital energies across the transition metals. Nonrelativistic quantum mechanics yields the wrong placement of several elements unless one adds empirical corrections or uses extremely sophisticated many-electron calculations. Even then, results often depend on approximations built to match experimental data. The same is true for bonding: quantum mechanics explains the idea of the covalent bond, but the shapes, stabilities, and reactivities of real molecules come from semiempirical models whose details are not uniquely dictated by first principles.
The 4s vs 3d puzzle is one of Scerri’s favorites. The textbook Aufbau says \(4s\) fills before \(3d\). But across the transition metals many ionization energies, spectroscopic term energies, and the ground-state configurations of ions contradict the simple order. For example:
- Ca: \([\mathrm{Ar}],4s^2\)
- Sc: \([\mathrm{Ar}],3d^1 4s^2\)
- Cr: \([\mathrm{Ar}],3d^5 4s^1\) (not \(3d^4 4s^2\))
- Cu: \([\mathrm{Ar}],3d^{10} 4s^1\) (not \(3d^9 4s^2\))
To know the correct ordering, you need detailed configuration interaction, electron correlation, and experimental input, not the \(n+\ell\) rule. (Other famous anomalies: Nb: \([\mathrm{Kr}],4d^4 5s^1\); Mo: \([\mathrm{Kr}],4d^5 5s^1\);Ru: \([\mathrm{Kr}],4d^7 5s^1\); Rh: \([\mathrm{Kr}],4d^8 5s^1\); Pd: \([\mathrm{Kr}],4d^{10}\) 5s is empty; and Ag: \([\mathrm{Kr}],4d^{10} 5s^1\).)
For Scerri, these examples show that chemistry draws strength from quantum mechanics but is not reducible to it in the strong philosophical sense. Chemistry needs physics, yet it also requires its own conceptual toolkit—periodicity, valence, orbitals, configurations, trends—that cannot simply be read off from the fundamental equations.