The Period Table VSI

Potassium-Argon reversal. Where should hydrogen appear? Why the actinides and lanthanides appear along the bottom. Quantum basis for the length of each row.

Theodor Benfey’s arrangement is an example of a continuous (spiral) table. First published in 1964, it explicitly showed the location of lanthanides and actinides. The elements form a two-dimensional spiral, starting from hydrogen, and folding their way around two peninsulas, the transition metals, and lanthanides and actinides.

Main Page

The Period Table

• Quantum mechanics and order by shells and options for electrons in each shell, p89-91, accounts for the number of elements in each row.
• The block at the bottom should fit in; moved for size-of-page reasons!
• Atomic mass order is different from atomic weight order, with reversals at TODO
• All to right table and other alternatives.
• Where should hydrogen go: top left or top right? All but one or only one electron in its outer shell.

Potassium-argon reversal

GPT

Revealed in weight

Despite having a higher atomic number, potassium (K) has a lower atomic weight than argon (Ar).

• Argon (atomic number 18) has an atomic weight of approximately 39.948 amu.
• Potassium (atomic number 19) has an atomic weight of about 39.098 amu.

This anomaly arises because the most abundant isotope of argon is argon-40, while potassium’s mass is lowered by the prevalence of lighter isotopes like potassium-39. Despite potassium having one more proton than argon (and thus would typically be expected to have a higher atomic weight), the isotopic composition and the relative abundance of those isotopes lead to potassium having a lower average atomic weight than argon.

Revealed in electron configuration

The argon-potassium reversal refers to an anomaly in the periodic table where the electron configuration of the elements argon (Ar) and potassium (K) doesn’t follow the expected order based on their atomic numbers. Normally, as you move across the periodic table, each element has one more proton and one more electron than the element before it, and electrons fill the available subshells in an order defined by their energy levels.

However, even though potassium has a higher atomic number than argon (19 vs. 18), the 3s and 3p subshells (which are fully filled in argon, giving it a noble gas configuration) have lower energy than the 4s subshell (into which the first electron of potassium goes). This might seem to suggest a ‘reversal’, as the 3d subshell is not filled before moving on to the 4s subshell, but this is actually due to the 4s subshell having a lower energy than the 3d subshell.

So, when you move from argon to potassium in the periodic table, the next electron does not go into the 3d subshell as might be expected if only considering the principal quantum number, but instead goes into the 4s subshell, following the actual order of energy levels. This is not a ‘reversal’ per se but a reflection of the complexities in electron configuration as atomic number increases, influenced by electron-electron repulsions, and the overall shape and energy of the atomic orbitals.

Electron Shells

GPT and cf. p88ff.

Here is how you determine the possible number of configurations in each electron shell.

Four quantum numbers describe the properties of electrons in an atom.

1. Principal Quantum Number (\(n\)): Determines the electron’s energy level or shell. It takes positive integer values \((1, 2, 3, \dots)\). Larger values of \(n\) correspond to higher energy levels.

2. Angular Momentum Quantum Number (\(l\)): Defines the shape of the electron’s orbital. It takes integer values from 0 to \(n - 1\) for each value of \(n\). For a given \(n\), \(l\) can be \(0, 1, \dots, n - 1\). Common names for orbitals with specific \(l\) values are: \(s\) (0), \(p\) (1), \(d\) (2), and \(f\) (3).

3. Magnetic Quantum Number (\(m_l\)): Describes the orientation of the orbital in space relative to the other orbitals. It takes integer values from \(-l\) to \(+l\), including zero. So for a given \(l\), \(m_l\) can be \(-l, -l+1, \dots, 0, \dots, l-1, l\).

4. Spin Quantum Number (\(m_s\)): Specifies the electron’s spin direction, which can be either \(+\frac{1}{2}\) or \(-\frac{1}{2}\). This quantum number indicates the intrinsic angular momentum of the electron.

These quantum numbers collectively define the unique quantum state of an electron in an atom, following the Pauli Exclusion Principle, which states that no two electrons can have the same set of four quantum numbers within the same atom.

Number of configurations

GPT cf. p90

Yes, based on the four quantum numbers, you can deduce a formula to calculate the number of electrons within a given shell of an atom. The principal quantum number (n) defines the shell, and the maximum number of electrons within a shell can be determined by the formula:

\(\text{Maximum number of electrons in a shell} = 2n^2\)

This formula arises because, for each energy level (n), there are n subshells, each subshell can hold up to \(4l + 2\) electrons (where \(l\) is the azimuthal quantum number), and when you sum this over all possible values of \(l\) for a given \(n\), you get \(2n^2\).

Here’s a table illustrating the number of electrons and possible configurations for each shell up to n=4:

Shell (n)	Maximum Electrons (2n²)	Subshells (l values)	Number of Orbitals	Electrons per Orbital Configuration
1	2	0 (s)	1 (1s)	2
2	8	0 (s), 1 (p)	4 (2s, 2p)	2 (2s), 6 (2p)
3	18	0 (s), 1 (p), 2 (d)	9 (3s, 3p, 3d)	2 (3s), 6 (3p), 10 (3d)
4	32	0 (s), 1 (p), 2 (d), 3 (f)	16 (4s, 4p, 4d, 4f)	2 (4s), 6 (4p), 10 (4d), 14 (4f)

• “Shell (n)” is the principal quantum number indicating the shell level.
• “Maximum Electrons (2n²)” shows the maximum number of electrons that can be accommodated in a given shell.
• “Subshells (l values)” lists the subshells available in each shell (s, p, d, f corresponding to l values 0, 1, 2, 3).
• “Number of Orbitals” indicates the total orbitals available in each subshell (each s has 1, p has 3, d has 5, and f has 7 orbitals).
• “Electrons per Orbital Configuration” shows the distribution of electrons in each type of orbital within the shell.

Each orbital can hold a maximum of 2 electrons, which is dictated by the Pauli exclusion principle and the spin quantum number, which can be +1/2 or -1/2.

Order of filling

GPT cf. p91

The order of orbital filling in an atom is determined by the Aufbau principle, which states that electrons are added to the lowest energy orbitals first before moving to higher energy orbitals. The order can be determined by the sum of the principal quantum number ((n)) and the azimuthal quantum number ((l)). Orbitals with a lower sum of (n + l) are filled before those with a higher sum. If two orbitals have the same (n + l) value, the one with the lower (n) is filled first.

Here’s the general order for filling orbitals:

1. 1s
2. 2s
3. 2p
4. 3s
5. 3p
6. 4s
7. 3d
8. 4p
9. 5s
10. 4d
11. 5p
12. 6s
13. 4f
14. 5d
15. 6p
16. 7s
17. 5f
18. 6d
19. 7p

To visualize this, you can refer to the periodic table or use the diagonal rule. Draw diagonal lines from the top to the bottom right across the table of s, p, d, and f blocks. The order in which these diagonal lines are drawn will give you the order of filling.

For example, the 4s subshell is filled before the 3d subshell because, even though they appear close in energy levels (especially as the atomic number increases), 4s has a slightly lower energy for elements in the first and second rows of the transition metals. However, after the 4s is filled and additional electrons are added to the 3d subshell, the 4s electrons are actually higher in energy than the 3d electrons due to electron-electron interactions and shielding.

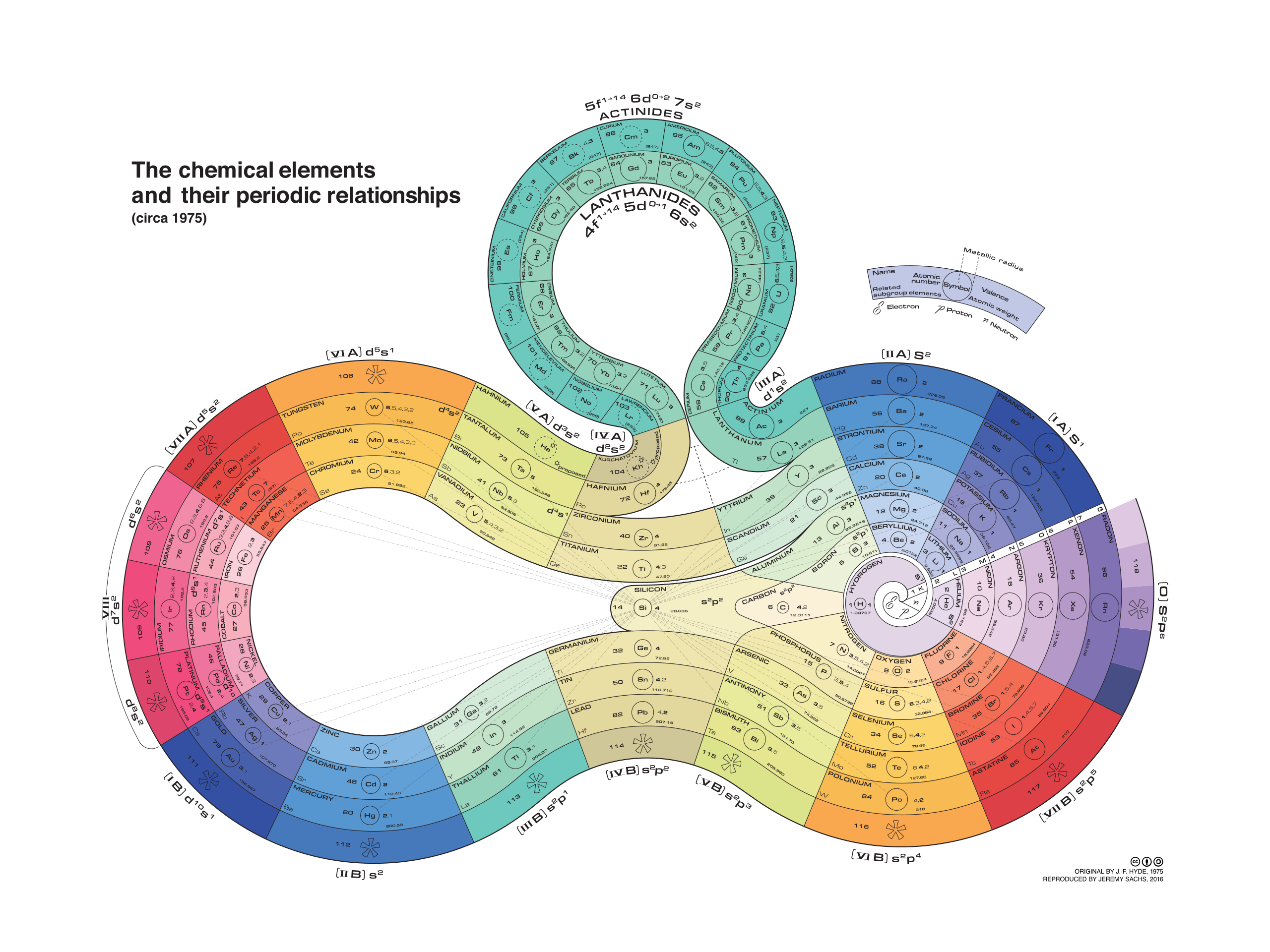
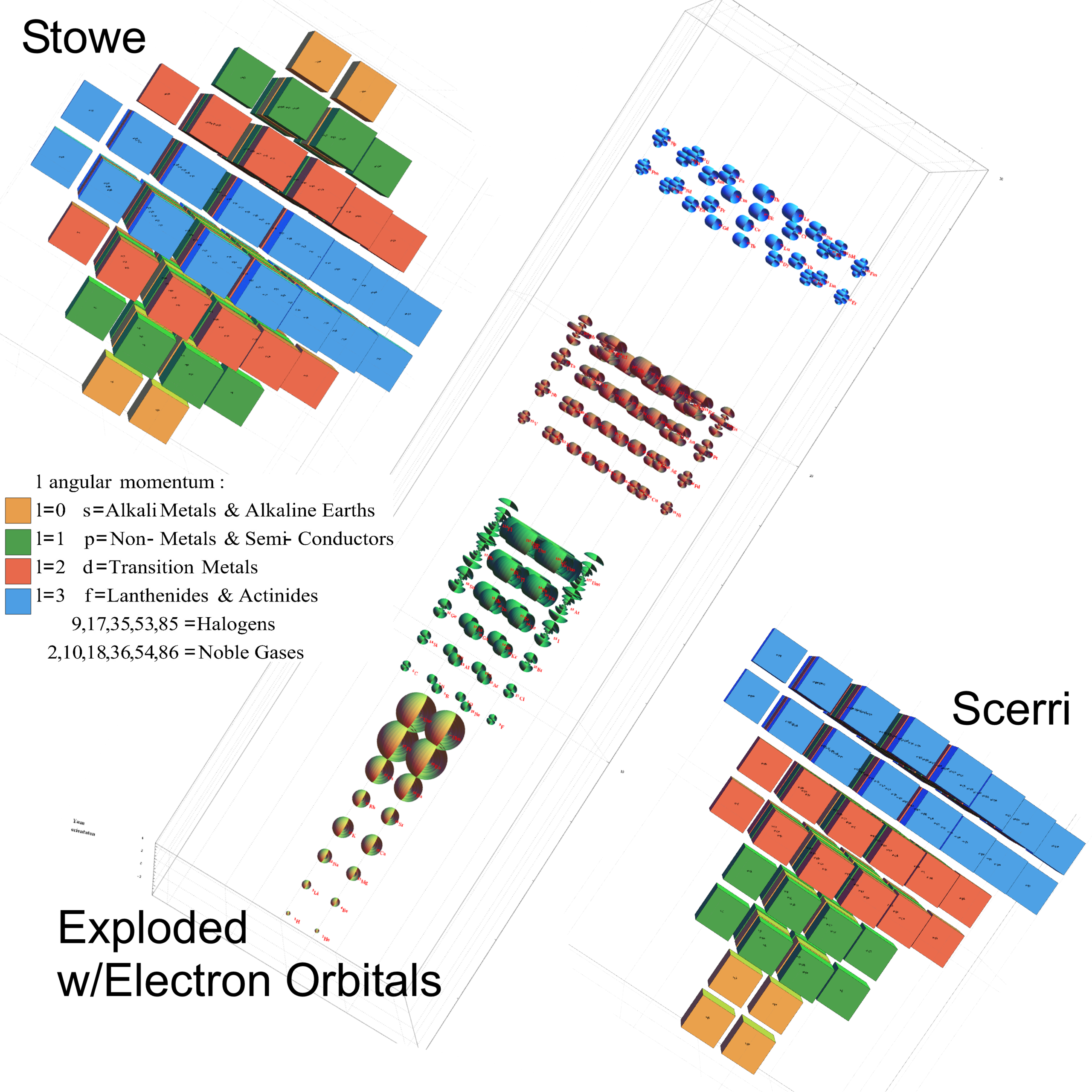
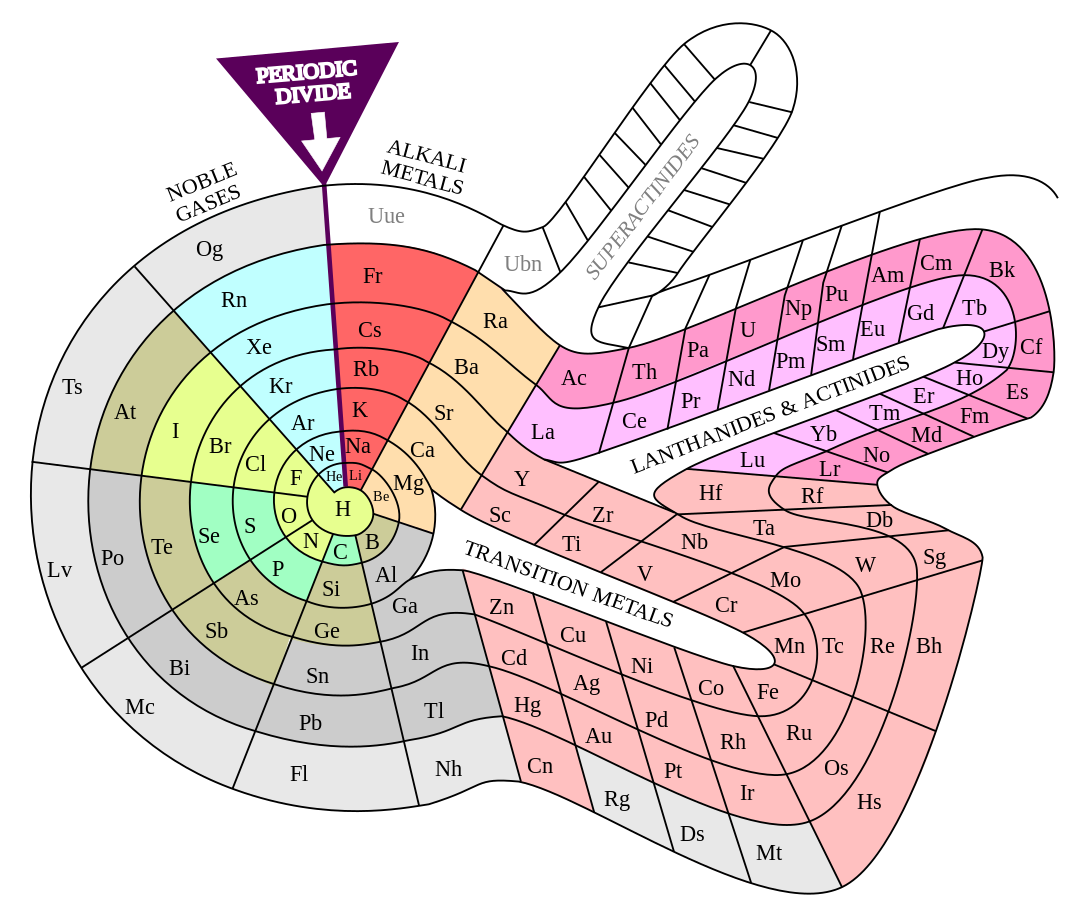
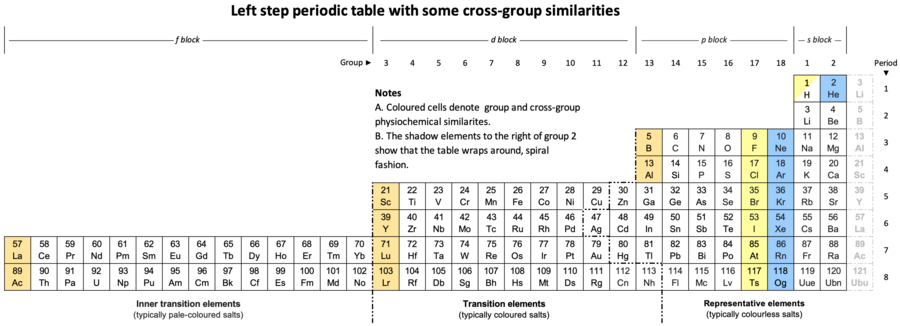
Alternative Period Table Presentations

Source: Wikipedia

A redrawn version of Kapustinsky’s triangular or step pyramid periodic table (1953).[26] Period 0 includes the electron and neutron. Each period repeats once. Two kinds of bilateral symmetry are present: shape; and metals and nonmetals in each half.

Left step periodic table with 33rd shadow column showing that the periods wrap around

Long table blocks in the conventional order: s-, f-, d- and p-

This has color coded 3D cut-away views of the spherical Schroedinger electron probability densities (making it 4D with 3D objects). The color is based on the l (angular momentum) quantum number. The X-Y-Z position is based n,m,s(pin) quantum numbers.

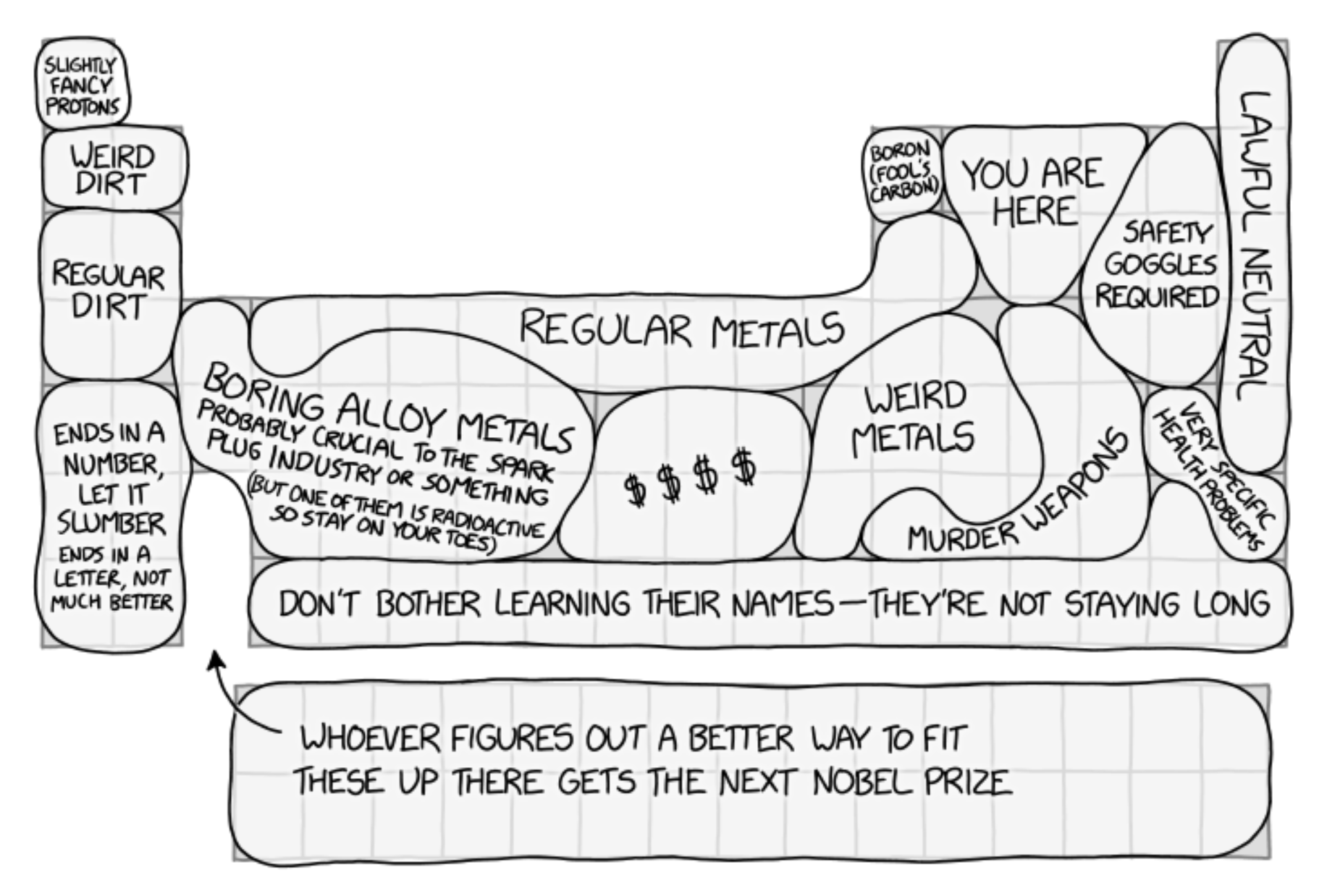
XKCD

Deets

• Eric Scerri
• Volume 289
• Published 2011

Theodor Benfey’s arrangement is an example of a continuous (spiral) table. First published in 1964, it explicitly showed the location of lanthanides and actinides. The elements form a two-dimensional spiral, starting from hydrogen, and folding their way around two peninsulas, the transition metals, and lanthanides and actinides. A redrawn version of Kapustinsky’s triangular or step pyramid periodic table (1953).[26] Period 0 includes the electron and neutron. Each period repeats once. Two kinds of bilateral symmetry are present: shape; and metals and nonmetals in each half. Left step periodic table with 33rd shadow column showing that the periods wrap around Long table blocks in the conventional order: s-, f-, d- and p- This has color coded 3D cut-away views of the spherical Schroedinger electron probability densities (making it 4D with 3D objects). The color is based on the l (angular momentum) quantum number. The X-Y-Z position is based n,m,s(pin) quantum numbers.