Discrete Case Study PIR Exhibits
Discrete (equal points) Book Case Study Results
Exhibits by Chapter
- Chapter 2: Basic loss statistics (A-C)
- Chapter 4: VaR, TVaR and EPD statistics (D, E)
- Chapter 7: Portfolio pricing, used for calibration (F, G)
- Chapter 9: Classical portfolio and stand-alone pricing (H-L)
- Chapter 11: Modern portfolio and stand-alone pricing (M-Q)
- Chapter 13: Classical allocations (R, S)
- Chapter 15: Modern allocations (T-Y)
See Section 1.28 for more details.
Table A
PIR Chapter 2, Tables 2.3, 2.5, 2.6, 2.7, Estimated mean, CV, skewness and kurtosis by line and in total, gross and net.
| statistic | Gross: X1 | Gross: X2 | Gross: Total | Net: X1 | Net: X2 | Net: Total |
|---|---|---|---|---|---|---|
| Mean | 4.75 | 22.75 | 27.5 | 4.75 | 5.25 | 10 |
| CV | 1.003 | 1.707 | 1.423 | 1.003 | 1.624 | 0.977 |
| Skewness | 0.016 | 1.154 | 1.129 | 0.016 | 1.147 | 0.765 |
| Kurtosis | -1.978 | -0.667 | -0.648 | -1.978 | -0.673 | -0.503 |
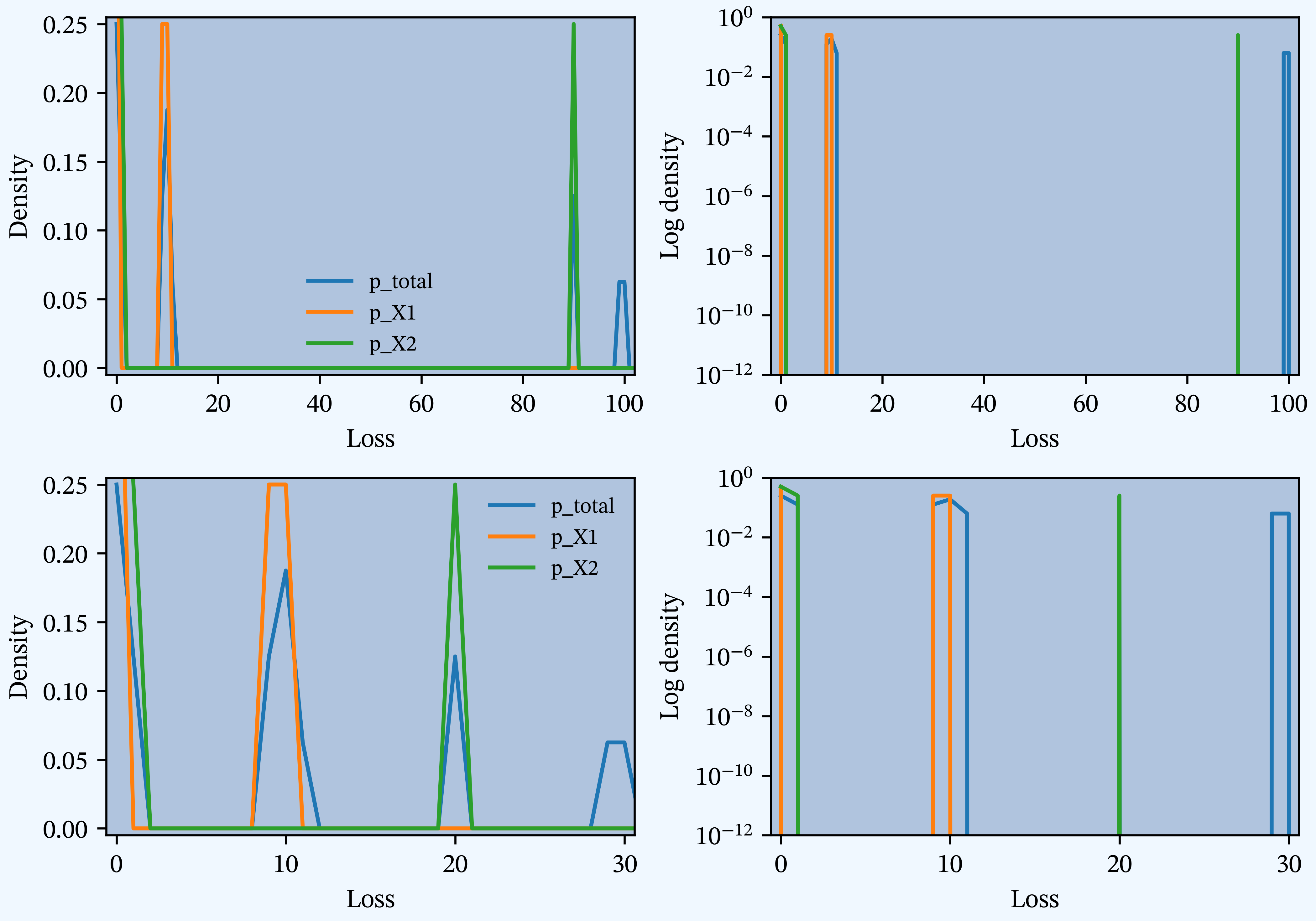
Figure B
PIR Chapter 2, Figures 2.2, 2.4, 2.6, Gross and net densities on a linear and log scale.
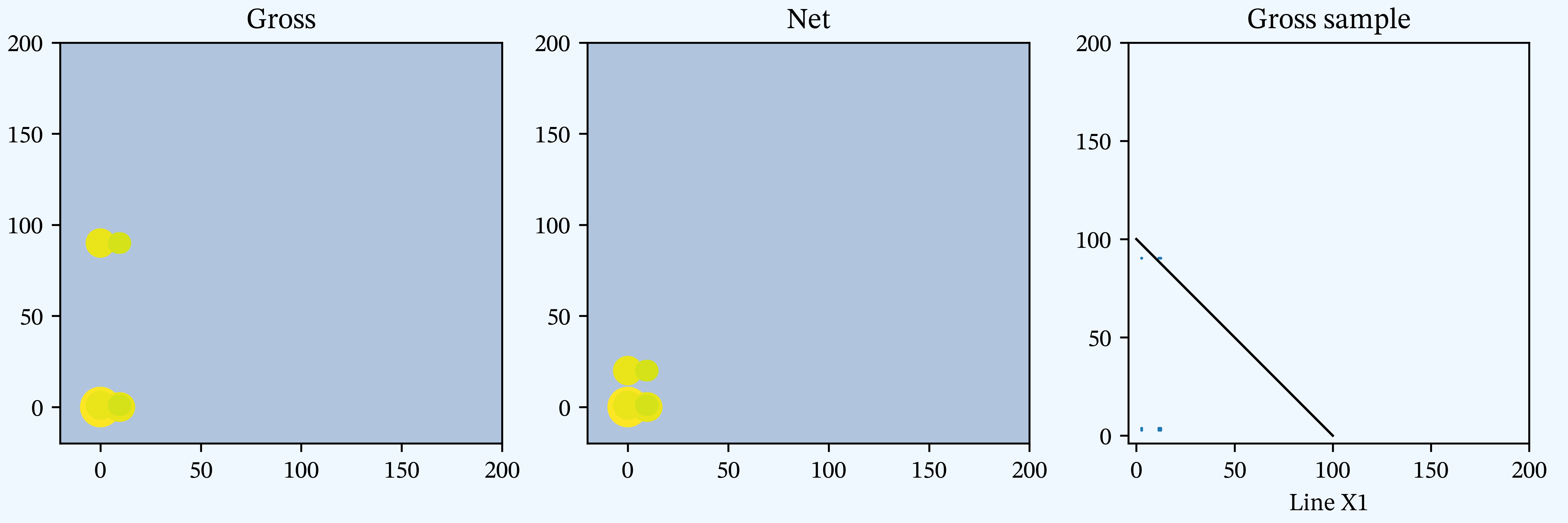
Figure C
PIR Chapter 2, Figures 2.3, 2.5, 2.7, Bivariate densities: gross and net with gross sample.
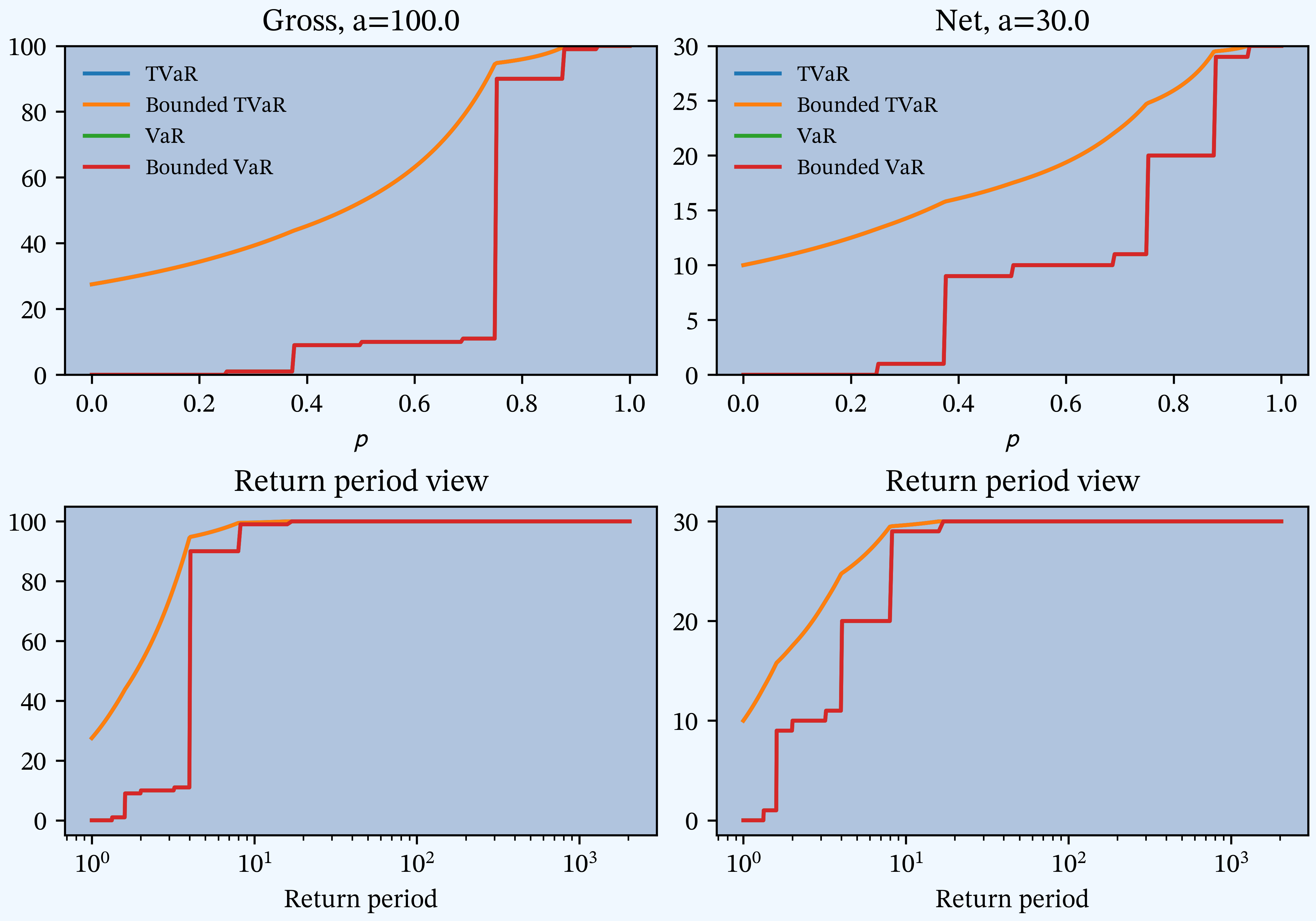
Figure D
PIR Chapter 4, Figures 4.9, 4.10, 4.11, 4.12, TVaR, and VaR for unlimited and limited variables, gross and net.
Table E
PIR Chapter 4, Tables 4.6, 4.7, 4.8, Estimated VaR, TVaR, and EPD by line and in total, gross, and net.
| statistic | Gross: X1 | Gross: X2 | Gross: Benefit | Gross: Sum | Gross: Total | Net: X1 | Net: X2 | Net: Benefit | Net: Sum | Net: Total |
|---|---|---|---|---|---|---|---|---|---|---|
| VaR 90.0 | 10 | 90 | 0.0101 | 100 | 99 | 10 | 20 | 0.0345 | 30 | 29 |
| VaR 95.0 | 10 | 90 | 0 | 100 | 100 | 10 | 20 | 0 | 30 | 30 |
| VaR 97.5 | 10 | 90 | 0 | 100 | 100 | 10 | 20 | 0 | 30 | 30 |
| VaR 99.0 | 10 | 90 | 0 | 100 | 100 | 10 | 20 | 0 | 30 | 30 |
| VaR 99.6 | 10 | 90 | 0 | 100 | 100 | 10 | 20 | 0 | 30 | 30 |
| VaR 99.9 | 10 | 90 | 0 | 100 | 100 | 10 | 20 | 0 | 30 | 30 |
| TVaR 90.0 | 10 | 90 | 0.00376 | 100 | 99.6 | 10 | 20 | 0.0127 | 30 | 29.6 |
| TVaR 95.0 | 10 | 90 | 0 | 100 | 100 | 10 | 20 | 0 | 30 | 30 |
| TVaR 97.5 | 10 | 90 | 0 | 100 | 100 | 10 | 20 | 0 | 30 | 30 |
| TVaR 99.0 | 10 | 90 | 0 | 100 | 100 | 10 | 20 | 0 | 30 | 30 |
| TVaR 99.6 | 10 | 90 | 0 | 100 | 100 | 10 | 20 | 0 | 30 | 30 |
| TVaR 99.9 | 10 | 90 | 0 | 100 | 100 | 10 | 20 | 0 | 30 | 30 |
| EPD 10.0 | 8.6 | 80.9 | 0.0681 | 89.5 | 83.8 | 8.6 | 17.9 | 0.23 | 26.4 | 21.5 |
| EPD 5.0 | 9 | 85.5 | 0.0588 | 94.5 | 89.2 | 9 | 18.9 | 0.098 | 28 | 25.5 |
| EPD 2.5 | 9.5 | 87.7 | 0.0346 | 97.2 | 94 | 9.5 | 19.5 | 0.0545 | 29 | 27.5 |
| EPD 1.0 | 9.8 | 89.1 | 0.0164 | 98.9 | 97.3 | 9.8 | 19.8 | 0.0314 | 29.6 | 28.7 |
| EPD 0.4 | 9.9 | 89.6 | 0.00953 | 99.6 | 98.6 | 9.9 | 19.9 | 0.0163 | 29.8 | 29.4 |
| EPD 0.1 | 10 | 89.9 | 0.00331 | 99.9 | 99.6 | 10 | 20 | 0.00402 | 30 | 29.8 |
Table F
PIR Chapter 7, Table 7.2, Pricing summary.
| stat | Gross | Net |
|---|---|---|
| Loss | 27.5 | 10 |
| Margin | 6.591 | 1.818 |
| Premium | 34.091 | 11.818 |
| Loss Ratio | 0.807 | 0.846 |
| Capital | 65.909 | 18.182 |
| Rate of Return | 0.1 | 0.1 |
| Assets | 100 | 30 |
| Leverage | 0.517 | 0.65 |
Table H
PIR Chapter 9, Tables 9.2, 9.5, 9.8, Classical pricing by method.
| method | Parameters: Value | X1: Net | X1: Gross | X2: Net | X2: Gross | Total: Net | Total: Gross | Total: Ceded |
|---|---|---|---|---|---|---|---|---|
| Net | 4.750 | 4.75 | 5.2 | 22.8 | 10 | 27.5 | 17.5 | |
| VaR | 0.750 | 9 | 1 | 1 | 11 | 11 | 0 | |
| Expected Value | 0.240 | 5.9 | 6.5 | 28.2 | 12.4 | 34.1 | 21.7 | |
| Variance | 0.004 | 4.848 | 5.6 | 29.2 | 10.4 | 34.1 | 23.7 | |
| Esscher | 0.004 | 4.84 | 5.5 | 29.3 | 10.4 | 34.1 | 23.7 | |
| Standard Deviation | 0.168 | 5.6 | 6.7 | 29.3 | 11.6 | 34.1 | 22.4 | |
| Semi-Variance | 0.006 | 4.816 | 5.6 | 29.3 | 10.3 | 34.1 | 23.7 | |
| Fischer | 0.196 | 5.4 | 6.7 | 29.3 | 11.5 | 34.1 | 22.6 | |
| Dutch | 0.392 | 5.7 | 6.7 | 29.3 | 11.5 | 34.1 | 22.6 |
Table I
PIR Chapter 9, Tables 9.3, 9.6, 9.9, Sum of parts (SoP) stand-alone vs. diversified classical pricing by method.
| method | Total: Gross | Total: Net | SoP: Gross | SoP: Net | Delta: Gross | Delta: Net |
|---|---|---|---|---|---|---|
| Net | 27.5 | 10 | 27.5 | 10 | 0 | 0 |
| VaR | 11 | 11 | 10 | 10 | -1 | -1 |
| Expected Value | 34.1 | 12.4 | 34.1 | 12.4 | 0 | 0 |
| Variance | 34.1 | 10.4 | 34.1 | 10.4 | 0 | 0 |
| Esscher | 34.1 | 10.4 | 34.1 | 10.4 | 0 | -0 |
| Standard Deviation | 34.1 | 11.6 | 34.8 | 12.2 | 0.753 | 0.594 |
| Semi-Variance | 34.1 | 10.3 | 34.1 | 10.4 | 0.033 | 0.033 |
| Fischer | 34.1 | 11.5 | 34.7 | 12.1 | 0.644 | 0.586 |
| Dutch | 34.1 | 11.5 | 35 | 12.4 | 0.931 | 0.907 |
Table J
PIR Chapter 9, Tables 9.4, 9.7, 9.10, Implied loss ratios from classical pricing by method.
| method | X1: Net | X1: Gross | X2: Net | X2: Gross | Total: Net | Total: Gross | Total: Ceded |
|---|---|---|---|---|---|---|---|
| Net | 1.000 | 1 | 1 | 1 | 1 | 1 | 1 |
| VaR | 0.528 | 5.2 | 22.8 | 0.909 | 2.5 | inf | |
| Expected Value | 0.807 | 0.807 | 0.807 | 0.807 | 0.807 | 0.807 | |
| Variance | 0.98 | 0.944 | 0.778 | 0.961 | 0.807 | 0.739 | |
| Esscher | 0.981 | 0.947 | 0.778 | 0.963 | 0.807 | 0.738 | |
| Standard Deviation | 0.855 | 0.785 | 0.777 | 0.859 | 0.807 | 0.78 | |
| Semi-Variance | 0.986 | 0.943 | 0.776 | 0.966 | 0.807 | 0.737 | |
| Fischer | 0.878 | 0.785 | 0.776 | 0.868 | 0.807 | 0.775 | |
| Dutch | 0.836 | 0.784 | 0.775 | 0.872 | 0.807 | 0.774 |
Table K
PIR Chapter 9, Table 9.11, Comparison of stand-alone and sum of parts premium.
| Gross SoP | Gross Total | Gross Redn | Net SoP | Net Total | Net Redn | |
|---|---|---|---|---|---|---|
| No Default: Loss | 27.5 | 27.5 | 0.0% | 1000.0% | 1000.0% | 0.0% |
| No Default: Premium | 34.1 | 34.1 | 0.0% | 11.8 | 11.8 | -0.0% |
| No Default: Capital | 65.9 | 65.9 | 0.0% | 18.2 | 18.2 | 0.0% |
| With Default: Loss | 27.5 | 27.5 | 0.0% | 1000.0% | 1000.0% | 0.0% |
| With Default: Premium | 34.1 | 34.1 | 0.0% | 11.8 | 11.8 | -0.0% |
| With Default: Capital | 65.9 | 65.9 | 0.0% | 18.2 | 18.2 | 0.0% |
Table L
PIR Chapter 9, Tables 9.12, 9.13, 9.14, Constant CoC pricing by unit for Case Study.
| Gross: X1 | Gross: X2 | Gross: SoP | Gross: Total | Net: X1 | Net: SoP | Net: Total | |
|---|---|---|---|---|---|---|---|
| No Default: Loss | 4.75 | 22.8 | 27.5 | 27.5 | 4.75 | 10 | 10 |
| No Default: Margin | 0.477 | 6.1 | 6.6 | 6.6 | 0.477 | 1.818 | 1.818 |
| No Default: Premium | 5.2 | 28.9 | 34.1 | 34.1 | 5.2 | 11.8 | 11.8 |
| No Default: Loss Ratio | 0.909 | 0.788 | 0.807 | 0.807 | 0.909 | 0.846 | 0.846 |
| No Default: Capital | 4.773 | 61.1 | 65.9 | 65.9 | 4.773 | 18.2 | 18.2 |
| No Default: Rate of Return | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| No Default: Leverage | 1.095 | 0.472 | 0.517 | 0.517 | 1.095 | 0.65 | 0.65 |
| No Default: Assets | 10 | 90 | 100 | 100 | 10 | 30 | 30 |
| With Default: Loss | 4.75 | 22.8 | 27.5 | 27.5 | 4.75 | 10 | 10 |
| With Default: Margin | 0.477 | 6.1 | 6.6 | 6.6 | 0.477 | 1.818 | 1.818 |
| With Default: Premium | 5.2 | 28.9 | 34.1 | 34.1 | 5.2 | 11.8 | 11.8 |
| With Default: Loss Ratio | 0.909 | 0.788 | 0.807 | 0.807 | 0.909 | 0.846 | 0.846 |
| With Default: Capital | 4.773 | 61.1 | 65.9 | 65.9 | 4.773 | 18.2 | 18.2 |
| With Default: Rate of Return | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| With Default: Leverage | 1.095 | 0.472 | 0.517 | 0.517 | 1.095 | 0.65 | 0.65 |
| With Default: Assets | 10 | 90 | 100 | 100 | 10 | 30 | 30 |
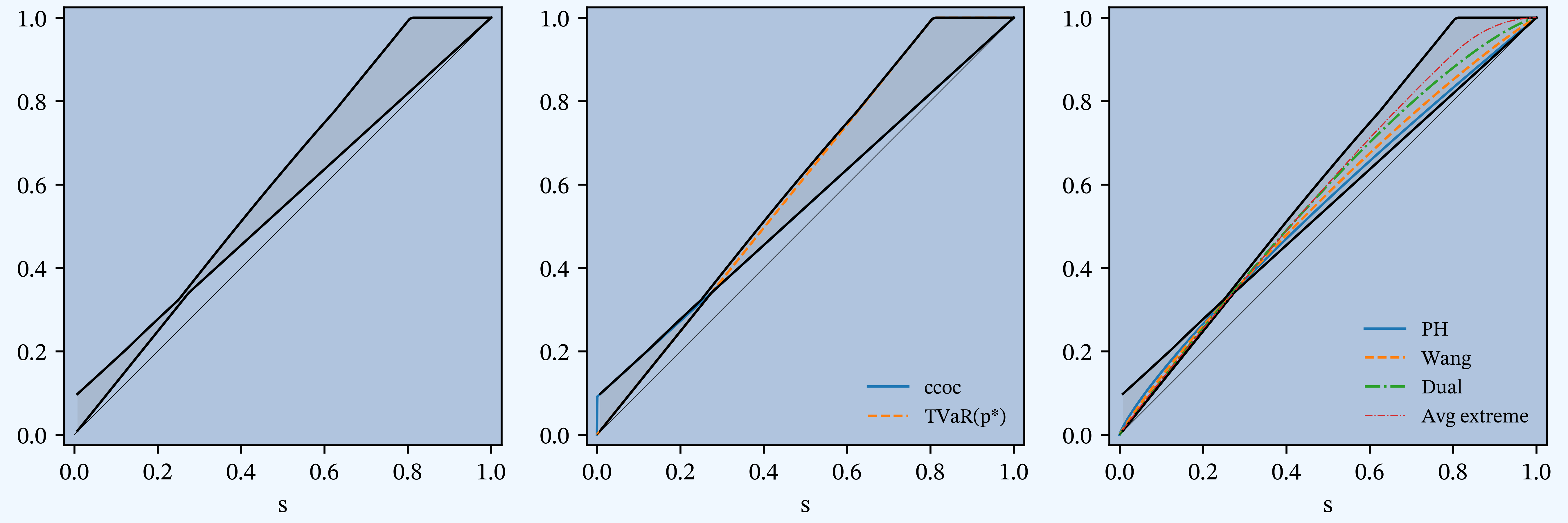
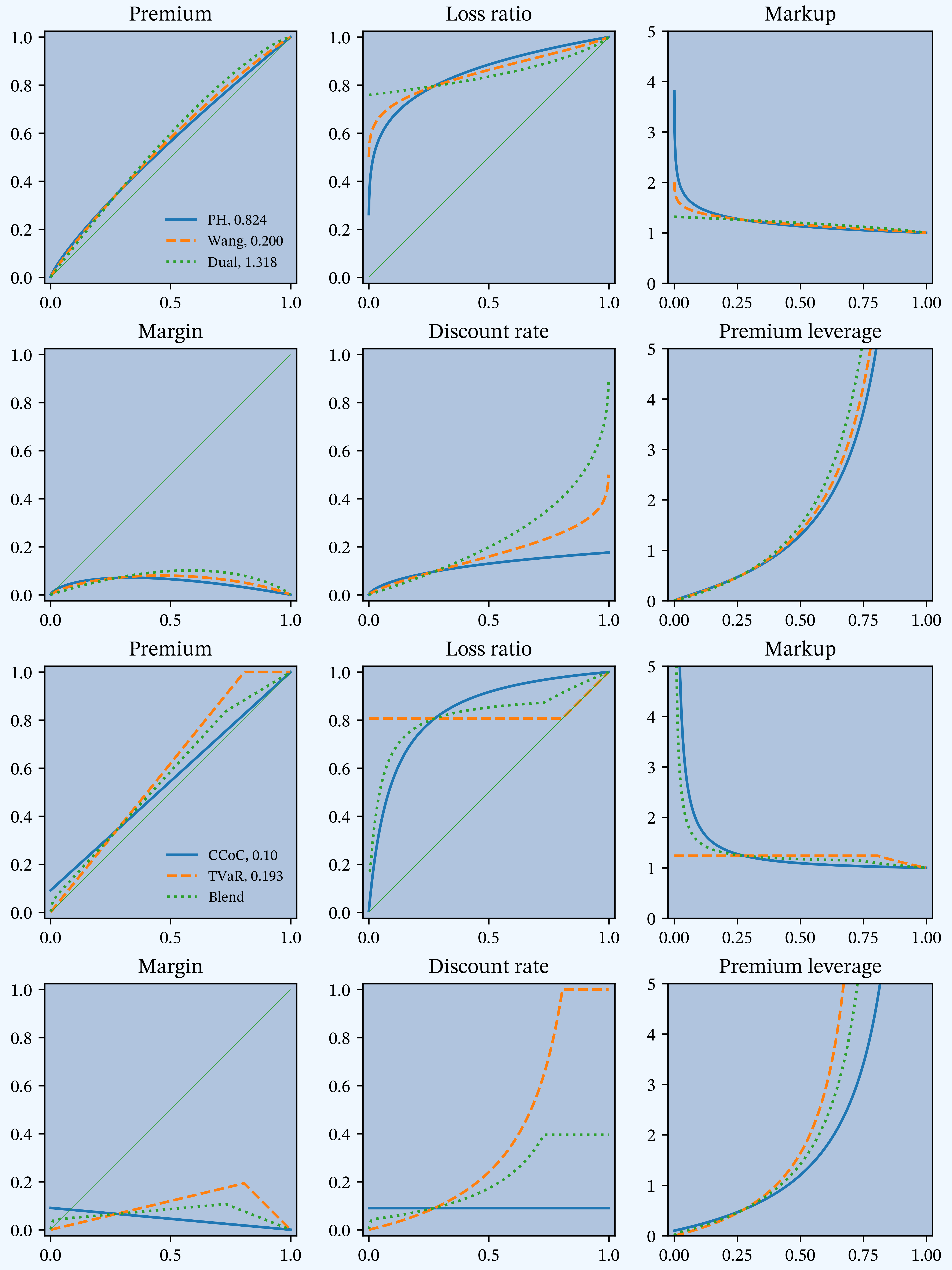
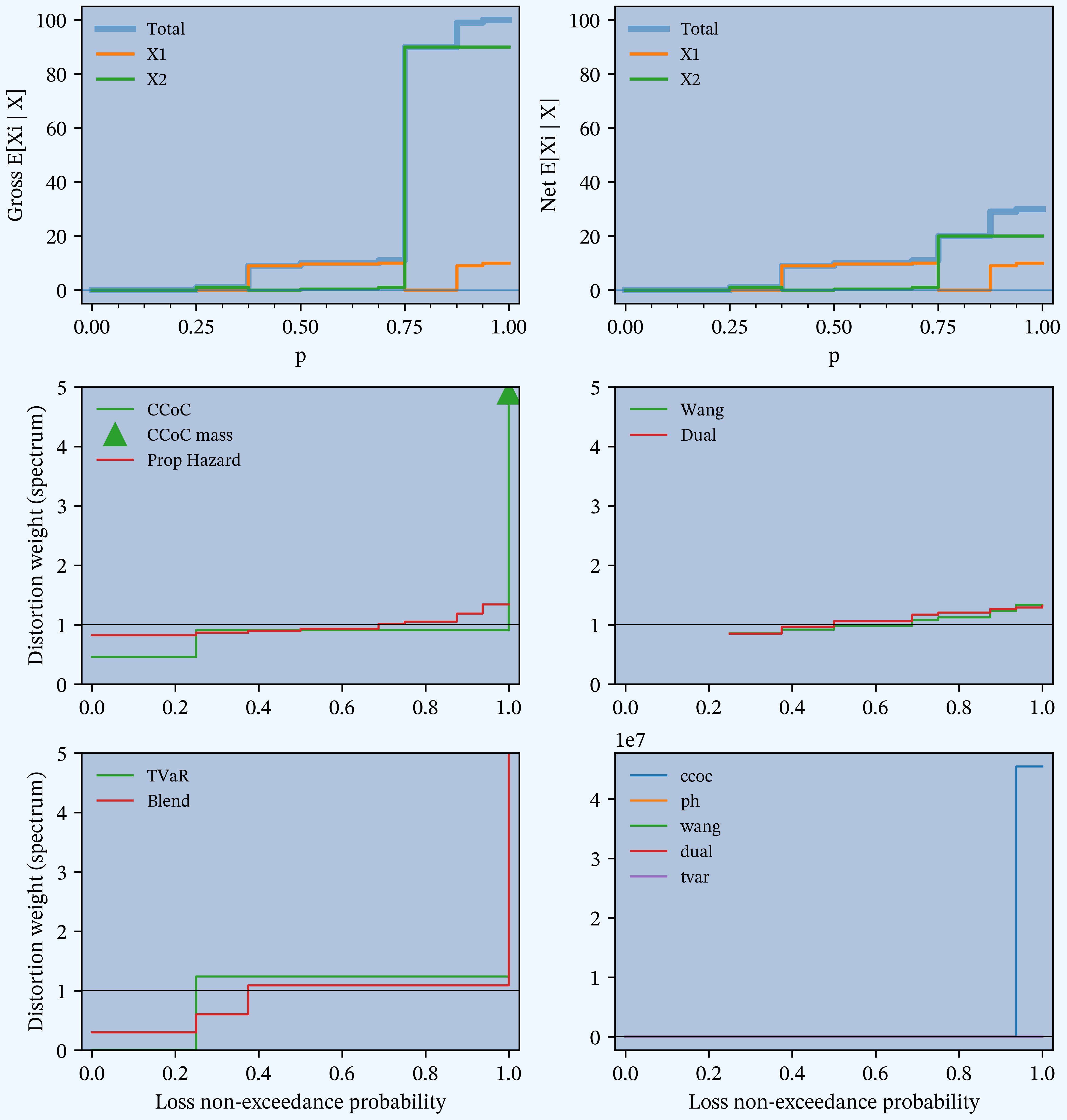
Figure M
PIR Chapter 11, Figures 11.2, 11.3, 11.4,11.5, Distortion envelope for Case Study, gross.
Table N
PIR Chapter 11, Table 11.5, Parameters for the six SRMs and associated distortions.
| method | Param | Error | Premium | K | Ι | S |
|---|---|---|---|---|---|---|
| Ccoc | 0.1 | 0 | 34.091 | 65.909 | 0.1 | 0 |
| PH | 0.824 | 0 | 34.091 | 65.909 | 0.1 | 0 |
| Wang | 0.2 | 0 | 34.091 | 65.909 | 0.1 | 0 |
| Dual | 1.318 | -0 | 34.091 | 65.909 | 0.1 | 0 |
| Tvar | 0.193 | 0 | 34.091 | 65.909 | 0.1 | 0 |
Figure O
PIR Chapter 11, Figures 11.6, 11.7, 11.8, Variation in insurance statistics for six distortions as \(s\) varies.
Figure P
PIR Chapter 11, Figures 11.9, 11.10, 11.11, Variation in insurance statistics as the asset limit is varied.
Table Q
PIR Chapter 11, Tables 11.7, 11.8, 11.9, Pricing by unit and distortion for Case Study.
| Gross: X1 | Gross: X2 | Gross: SoP | Gross: Total | Net: X1 | Net: SoP | Net: Total | |
|---|---|---|---|---|---|---|---|
| Loss: Ccoc | 4.75 | 22.75 | 27.5 | 27.5 | 4.75 | 10 | 10 |
| Margin: Ccoc | 0.477 | 6.114 | 6.591 | 6.591 | 0.477 | 1.818 | 1.818 |
| Margin: PH | 0.652 | 6.205 | 6.857 | 6.591 | 0.652 | 2.028 | 1.762 |
| Margin: Wang | 0.782 | 6.107 | 6.889 | 6.591 | 0.782 | 2.149 | 1.85 |
| Margin: Dual | 0.955 | 5.93 | 6.885 | 6.591 | 0.955 | 2.299 | 2.004 |
| Margin: TVaR | 1.138 | 5.452 | 6.591 | 6.591 | 1.138 | 2.397 | 2.397 |
| Margin: Blend | 0.839 | 5.762 | 6.601 | 6.591 | 0.839 | 2.137 | 2.127 |
| Premium: Ccoc | 5.227 | 28.864 | 34.091 | 34.091 | 5.227 | 11.818 | 11.818 |
| Premium: PH | 5.402 | 28.955 | 34.357 | 34.091 | 5.402 | 12.028 | 11.762 |
| Premium: Wang | 5.532 | 28.857 | 34.389 | 34.091 | 5.532 | 12.149 | 11.85 |
| Premium: Dual | 5.705 | 28.68 | 34.385 | 34.091 | 5.705 | 12.299 | 12.004 |
| Premium: TVaR | 5.888 | 28.202 | 34.091 | 34.091 | 5.888 | 12.397 | 12.397 |
| Premium: Blend | 5.589 | 28.512 | 34.101 | 34.091 | 5.589 | 12.137 | 12.127 |
| Loss Ratio: Ccoc | 0.909 | 0.788 | 0.807 | 0.807 | 0.909 | 0.846 | 0.846 |
| Loss Ratio: PH | 0.879 | 0.786 | 0.8 | 0.807 | 0.879 | 0.831 | 0.85 |
| Loss Ratio: Wang | 0.859 | 0.788 | 0.8 | 0.807 | 0.859 | 0.823 | 0.844 |
| Loss Ratio: Dual | 0.833 | 0.793 | 0.8 | 0.807 | 0.833 | 0.813 | 0.833 |
| Loss Ratio: TVaR | 0.807 | 0.807 | 0.807 | 0.807 | 0.807 | 0.807 | 0.807 |
| Loss Ratio: Blend | 0.85 | 0.798 | 0.806 | 0.807 | 0.85 | 0.824 | 0.825 |
| Capital: Ccoc | 4.773 | 61.136 | 65.909 | 65.909 | 4.773 | 18.182 | 18.182 |
| Capital: PH | 4.598 | 61.045 | 65.643 | 65.909 | 4.598 | 17.972 | 18.238 |
| Capital: Wang | 4.468 | 61.143 | 65.611 | 65.909 | 4.468 | 17.851 | 18.15 |
| Capital: Dual | 4.295 | 61.32 | 65.615 | 65.909 | 4.295 | 17.701 | 17.996 |
| Capital: TVaR | 4.112 | 61.798 | 65.909 | 65.909 | 4.112 | 17.603 | 17.603 |
| Capital: Blend | 4.411 | 61.488 | 65.899 | 65.909 | 4.411 | 17.863 | 17.873 |
| Rate of Return: Ccoc | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Rate of Return: PH | 0.142 | 0.102 | 0.104 | 0.1 | 0.142 | 0.113 | 0.097 |
| Rate of Return: Wang | 0.175 | 0.1 | 0.105 | 0.1 | 0.175 | 0.12 | 0.102 |
| Rate of Return: Dual | 0.222 | 0.097 | 0.105 | 0.1 | 0.222 | 0.13 | 0.111 |
| Rate of Return: TVaR | 0.277 | 0.088 | 0.1 | 0.1 | 0.277 | 0.136 | 0.136 |
| Rate of Return: Blend | 0.19 | 0.094 | 0.1 | 0.1 | 0.19 | 0.12 | 0.119 |
| Leverage: Ccoc | 1.095 | 0.472 | 0.517 | 0.517 | 1.095 | 0.65 | 0.65 |
| Leverage: PH | 1.175 | 0.474 | 0.523 | 0.517 | 1.175 | 0.669 | 0.645 |
| Leverage: Wang | 1.238 | 0.472 | 0.524 | 0.517 | 1.238 | 0.681 | 0.653 |
| Leverage: Dual | 1.328 | 0.468 | 0.524 | 0.517 | 1.328 | 0.695 | 0.667 |
| Leverage: TVaR | 1.432 | 0.456 | 0.517 | 0.517 | 1.432 | 0.704 | 0.704 |
| Leverage: Blend | 1.267 | 0.464 | 0.517 | 0.517 | 1.267 | 0.679 | 0.679 |
| Assets: Ccoc | 10 | 90 | 100 | 100 | 10 | 30 | 30 |
Table R
PIR Chapter 13, Table 13.1, Comparison of gross expected losses by Case, catastrophe-prone lines.
| Unit | a | E[Xi(a)] | E[Xi ∧ ai] |
|---|---|---|---|
| X1 | 10 | 4.75 | 4.75 |
| X2 | 90 | 22.75 | 22.75 |
| Total | 100 | 27.5 | 27.5 |
| SoP | 100 | 27.5 | 27.5 |
Table S
PIR Chapter 13, Tables 13.2, 13.3, 13.4, Constant 0.10 ROE pricing for Case Study, classical PCP methods.
| Gross: X1 | Gross: X2 | Gross: Total | Net: X1 | Net: X2 | Net: Total | Ceded: Diff | |
|---|---|---|---|---|---|---|---|
| Loss: Expected Loss | 4.75 | 22.75 | 27.5 | 4.75 | 5.25 | 10 | 17.5 |
| Margin: Expected Loss | 1.138 | 5.452 | 6.591 | 0.864 | 0.955 | 1.818 | 4.773 |
| Margin: Scaled EPD | 0.477 | 6.114 | 6.591 | 0.477 | 1.341 | 1.818 | 4.773 |
| Margin: Scaled TVaR | 0.477 | 6.114 | 6.591 | 0.477 | 1.341 | 1.818 | 4.773 |
| Margin: Scaled VaR | 0.477 | 6.114 | 6.591 | 0.477 | 1.341 | 1.818 | 4.773 |
| Margin: Equal Risk EPD | 0.477 | 6.114 | 6.591 | 0.477 | 1.341 | 1.818 | 4.773 |
| Margin: Equal Risk TVaR | 0.477 | 6.114 | 6.591 | 0.477 | 1.341 | 1.818 | 4.773 |
| Margin: Equal Risk VaR | 0.477 | 6.114 | 6.591 | 0.477 | 1.341 | 1.818 | 4.773 |
| Margin: coTVaR | nan | nan | nan | nan | nan | nan | nan |
| Margin: Covar | 0.098 | 6.493 | 6.591 | 0.433 | 1.386 | 1.818 | 4.773 |
| Premium: Expected Loss | 5.888 | 28.202 | 34.091 | 5.614 | 6.205 | 11.818 | 22.273 |
| Premium: Scaled EPD | 5.227 | 28.864 | 34.091 | 5.227 | 6.591 | 11.818 | 22.273 |
| Premium: Scaled TVaR | 5.227 | 28.864 | 34.091 | 5.227 | 6.591 | 11.818 | 22.273 |
| Premium: Scaled VaR | 5.227 | 28.864 | 34.091 | 5.227 | 6.591 | 11.818 | 22.273 |
| Premium: Equal Risk EPD | 5.227 | 28.864 | 34.091 | 5.227 | 6.591 | 11.818 | 22.273 |
| Premium: Equal Risk TVaR | 5.227 | 28.864 | 34.091 | 5.227 | 6.591 | 11.818 | 22.273 |
| Premium: Equal Risk VaR | 5.227 | 28.864 | 34.091 | 5.227 | 6.591 | 11.818 | 22.273 |
| Premium: coTVaR | nan | nan | nan | nan | nan | nan | nan |
| Premium: Covar | 4.848 | 29.243 | 34.091 | 5.183 | 6.636 | 11.818 | 22.273 |
| Loss Ratio: Expected Loss | 0.807 | 0.807 | 0.807 | 0.846 | 0.846 | 0.846 | 0.786 |
| Loss Ratio: Scaled EPD | 0.909 | 0.788 | 0.807 | 0.909 | 0.797 | 0.846 | 0.786 |
| Loss Ratio: Scaled TVaR | 0.909 | 0.788 | 0.807 | 0.909 | 0.797 | 0.846 | 0.786 |
| Loss Ratio: Scaled VaR | 0.909 | 0.788 | 0.807 | 0.909 | 0.797 | 0.846 | 0.786 |
| Loss Ratio: Equal Risk EPD | 0.909 | 0.788 | 0.807 | 0.909 | 0.797 | 0.846 | 0.786 |
| Loss Ratio: Equal Risk TVaR | 0.909 | 0.788 | 0.807 | 0.909 | 0.797 | 0.846 | 0.786 |
| Loss Ratio: Equal Risk VaR | 0.909 | 0.788 | 0.807 | 0.909 | 0.797 | 0.846 | 0.786 |
| Loss Ratio: coTVaR | nan | nan | nan | nan | nan | nan | nan |
| Loss Ratio: Covar | 0.98 | 0.778 | 0.807 | 0.917 | 0.791 | 0.846 | 0.786 |
| Capital: Expected Loss | 11.384 | 54.525 | 65.909 | 8.636 | 9.545 | 18.182 | 47.727 |
| Capital: Scaled EPD | 4.773 | 61.136 | 65.909 | 4.773 | 13.409 | 18.182 | 47.727 |
| Capital: Scaled TVaR | 4.773 | 61.136 | 65.909 | 4.773 | 13.409 | 18.182 | 47.727 |
| Capital: Scaled VaR | 4.773 | 61.136 | 65.909 | 4.773 | 13.409 | 18.182 | 47.727 |
| Capital: Equal Risk EPD | 4.773 | 61.136 | 65.909 | 4.773 | 13.409 | 18.182 | 47.727 |
| Capital: Equal Risk TVaR | 4.773 | 61.136 | 65.909 | 4.773 | 13.409 | 18.182 | 47.727 |
| Capital: Equal Risk VaR | 4.773 | 61.136 | 65.909 | 4.773 | 13.409 | 18.182 | 47.727 |
| Capital: coTVaR | nan | nan | nan | nan | nan | nan | nan |
| Capital: Covar | 0.977 | 64.932 | 65.909 | 4.325 | 13.857 | 18.182 | 47.727 |
| Rate of Return: Expected Loss | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Rate of Return: Scaled EPD | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Rate of Return: Scaled TVaR | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Rate of Return: Scaled VaR | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Rate of Return: Equal Risk EPD | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Rate of Return: Equal Risk TVaR | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Rate of Return: Equal Risk VaR | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Rate of Return: coTVaR | nan | nan | nan | nan | nan | nan | nan |
| Rate of Return: Covar | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Leverage: Expected Loss | 0.517 | 0.517 | 0.517 | 0.65 | 0.65 | 0.65 | 0.467 |
| Leverage: Scaled EPD | 1.095 | 0.472 | 0.517 | 1.095 | 0.492 | 0.65 | 0.467 |
| Leverage: Scaled TVaR | 1.095 | 0.472 | 0.517 | 1.095 | 0.492 | 0.65 | 0.467 |
| Leverage: Scaled VaR | 1.095 | 0.472 | 0.517 | 1.095 | 0.492 | 0.65 | 0.467 |
| Leverage: Equal Risk EPD | 1.095 | 0.472 | 0.517 | 1.095 | 0.492 | 0.65 | 0.467 |
| Leverage: Equal Risk TVaR | 1.095 | 0.472 | 0.517 | 1.095 | 0.492 | 0.65 | 0.467 |
| Leverage: Equal Risk VaR | 1.095 | 0.472 | 0.517 | 1.095 | 0.492 | 0.65 | 0.467 |
| Leverage: coTVaR | nan | nan | nan | nan | nan | nan | nan |
| Leverage: Covar | 4.961 | 0.45 | 0.517 | 1.198 | 0.479 | 0.65 | 0.467 |
| Assets: Expected Loss | 17.273 | 82.727 | 100 | 14.25 | 15.75 | 30 | 70 |
| Assets: Scaled EPD | 10 | 90 | 100 | 10 | 20 | 30 | 70 |
| Assets: Scaled TVaR | 10 | 90 | 100 | 10 | 20 | 30 | 70 |
| Assets: Scaled VaR | 10 | 90 | 100 | 10 | 20 | 30 | 70 |
| Assets: Equal Risk EPD | 10 | 90 | 100 | 10 | 20 | 30 | 70 |
| Assets: Equal Risk TVaR | 10 | 90 | 100 | 10 | 20 | 30 | 70 |
| Assets: Equal Risk VaR | 10 | 90 | 100 | 10 | 20 | 30 | 70 |
| Assets: coTVaR | nan | nan | nan | nan | nan | nan | nan |
| Assets: Covar | 5.825 | 94.175 | 100 | 9.508 | 20.492 | 30 | 70 |
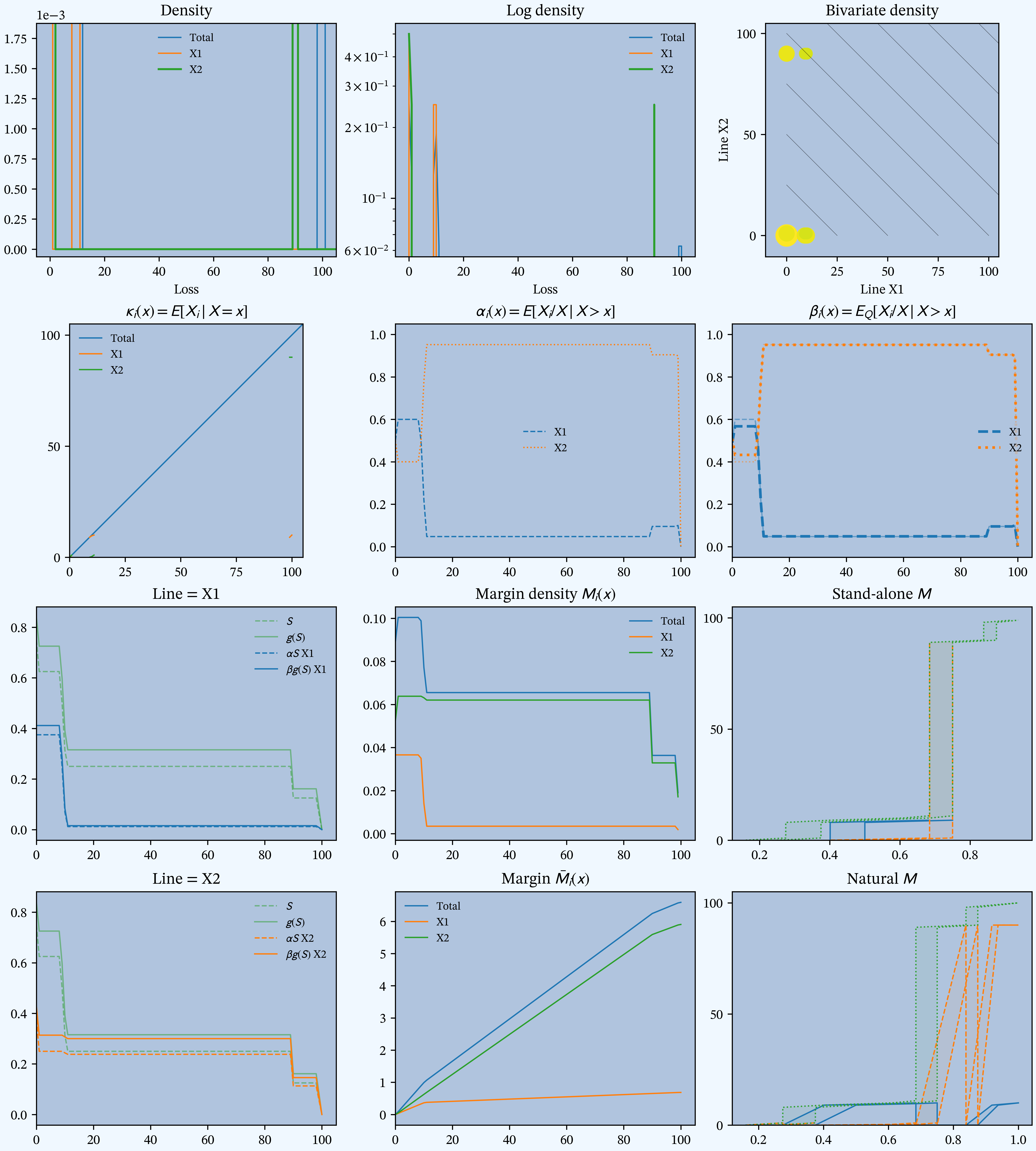
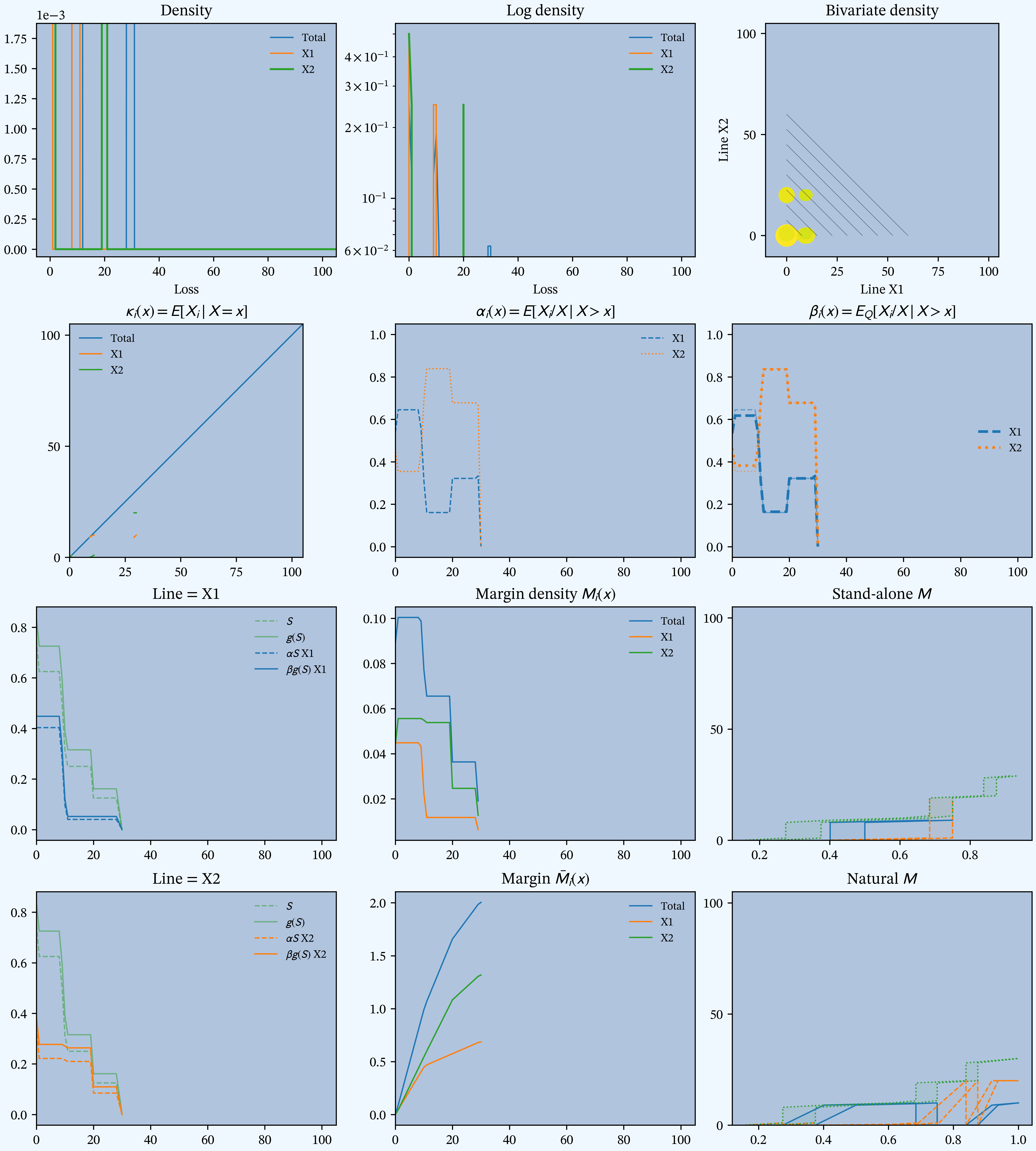
Figure T_gross
Figure T_net
Figure U
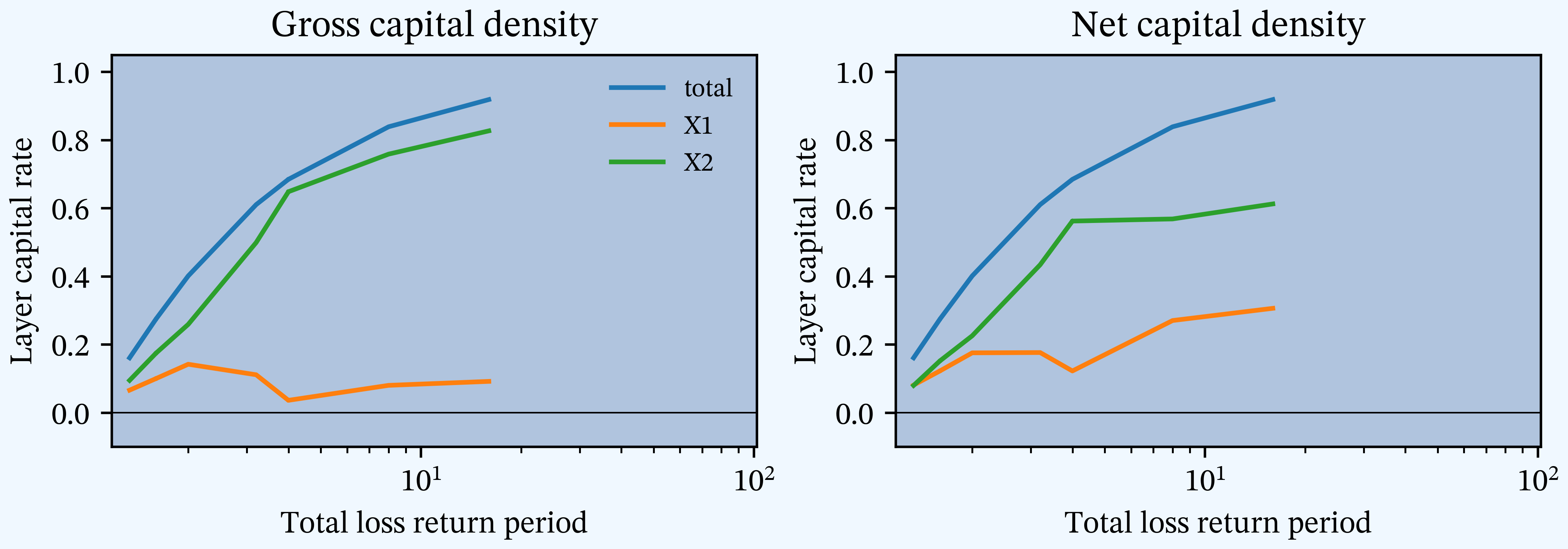
PIR Chapter 15, Figures 15.8, 15.9, 15.10, Capital density by layer.
Table V
PIR Chapter 15, Tables 15.35, 15.36, 15.37, Constant 0.10 ROE pricing for Cat/Non-Cat Case Study, distortion, SRM methods.
| Gross: X1 | Gross: X2 | Gross: Total | Net: X1 | Net: X2 | Net: Total | Ceded: Diff | |
|---|---|---|---|---|---|---|---|
| Loss: Expected Loss | 4.75 | 22.75 | 27.5 | 4.75 | 5.25 | 10 | 17.5 |
| Margin: Expected Loss | 1.138 | 5.45 | 6.59 | 0.864 | 0.955 | 1.818 | 4.773 |
| Margin: Dist Ccoc | 0.477 | 6.11 | 6.59 | 0.477 | 1.341 | 1.818 | 4.773 |
| Margin: Dist PH | 0.397 | 6.19 | 6.59 | 0.397 | 1.365 | 1.762 | 4.829 |
| Margin: Dist Wang | 0.502 | 6.09 | 6.59 | 0.502 | 1.349 | 1.85 | 4.74 |
| Margin: Dist Dual | 0.686 | 5.9 | 6.59 | 0.686 | 1.318 | 2.004 | 4.587 |
| Margin: Dist Tvar | 1.138 | 5.45 | 6.59 | 1.138 | 1.258 | 2.397 | 4.194 |
| Margin: Dist Blend | 0.839 | 5.75 | 6.59 | 0.839 | 1.288 | 2.127 | 4.464 |
| Premium: Expected Loss | 5.89 | 28.2 | 34.09 | 5.61 | 6.2 | 11.82 | 22.27 |
| Premium: Dist Ccoc | 5.23 | 28.86 | 34.09 | 5.23 | 6.59 | 11.82 | 22.27 |
| Premium: Dist PH | 5.15 | 28.94 | 34.09 | 5.15 | 6.61 | 11.76 | 22.33 |
| Premium: Dist Wang | 5.25 | 28.84 | 34.09 | 5.25 | 6.6 | 11.85 | 22.24 |
| Premium: Dist Dual | 5.44 | 28.65 | 34.09 | 5.44 | 6.57 | 12 | 22.09 |
| Premium: Dist Tvar | 5.89 | 28.2 | 34.09 | 5.89 | 6.51 | 12.4 | 21.69 |
| Premium: Dist Blend | 5.59 | 28.5 | 34.09 | 5.59 | 6.54 | 12.13 | 21.96 |
| Loss Ratio: Expected Loss | 0.807 | 0.807 | 0.807 | 0.846 | 0.846 | 0.846 | 0.786 |
| Loss Ratio: Dist Ccoc | 0.909 | 0.788 | 0.807 | 0.909 | 0.797 | 0.846 | 0.786 |
| Loss Ratio: Dist PH | 0.923 | 0.786 | 0.807 | 0.923 | 0.794 | 0.85 | 0.784 |
| Loss Ratio: Dist Wang | 0.904 | 0.789 | 0.807 | 0.904 | 0.796 | 0.844 | 0.787 |
| Loss Ratio: Dist Dual | 0.874 | 0.794 | 0.807 | 0.874 | 0.799 | 0.833 | 0.792 |
| Loss Ratio: Dist Tvar | 0.807 | 0.807 | 0.807 | 0.807 | 0.807 | 0.807 | 0.807 |
| Loss Ratio: Dist Blend | 0.85 | 0.798 | 0.807 | 0.85 | 0.803 | 0.825 | 0.797 |
| Capital: Expected Loss | 11.38 | 54.52 | 65.91 | 8.64 | 9.55 | 18.18 | 47.73 |
| Capital: Dist Ccoc | 4.773 | 61.14 | 65.91 | 4.773 | 13.41 | 18.18 | 47.73 |
| Capital: Dist PH | 4.549 | 61.36 | 65.91 | 4.73 | 13.51 | 18.24 | 47.67 |
| Capital: Dist Wang | 4.848 | 61.06 | 65.91 | 5.1 | 13.05 | 18.15 | 47.76 |
| Capital: Dist Dual | 4.804 | 61.11 | 65.91 | 5.25 | 12.74 | 18 | 47.91 |
| Capital: Dist Tvar | 4.861 | 61.05 | 65.91 | 5.36 | 12.25 | 17.6 | 48.31 |
| Capital: Dist Blend | 6.39 | 59.52 | 65.91 | 6.03 | 11.84 | 17.87 | 48.04 |
| Rate of Return: Expected Loss | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Rate of Return: Dist Ccoc | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Rate of Return: Dist PH | 0.087 | 0.101 | 0.1 | 0.084 | 0.101 | 0.097 | 0.101 |
| Rate of Return: Dist Wang | 0.104 | 0.1 | 0.1 | 0.098 | 0.103 | 0.102 | 0.099 |
| Rate of Return: Dist Dual | 0.143 | 0.097 | 0.1 | 0.131 | 0.103 | 0.111 | 0.096 |
| Rate of Return: Dist Tvar | 0.234 | 0.089 | 0.1 | 0.213 | 0.103 | 0.136 | 0.087 |
| Rate of Return: Dist Blend | 0.131 | 0.097 | 0.1 | 0.139 | 0.109 | 0.119 | 0.093 |
| Leverage: Expected Loss | 0.517 | 0.517 | 0.517 | 0.65 | 0.65 | 0.65 | 0.467 |
| Leverage: Dist Ccoc | 1.095 | 0.472 | 0.517 | 1.095 | 0.492 | 0.65 | 0.467 |
| Leverage: Dist PH | 1.132 | 0.472 | 0.517 | 1.088 | 0.49 | 0.645 | 0.468 |
| Leverage: Dist Wang | 1.083 | 0.472 | 0.517 | 1.03 | 0.506 | 0.653 | 0.466 |
| Leverage: Dist Dual | 1.132 | 0.469 | 0.517 | 1.035 | 0.516 | 0.667 | 0.461 |
| Leverage: Dist Tvar | 1.211 | 0.462 | 0.517 | 1.099 | 0.531 | 0.704 | 0.449 |
| Leverage: Dist Blend | 0.875 | 0.479 | 0.517 | 0.927 | 0.552 | 0.679 | 0.457 |
| Assets: Expected Loss | 17.27 | 82.73 | 100 | 14.25 | 15.75 | 30 | 70 |
| Assets: Dist Ccoc | 10 | 90 | 100 | 10 | 20 | 30 | 70 |
| Assets: Dist PH | 9.7 | 90.3 | 100 | 9.88 | 20.12 | 30 | 70 |
| Assets: Dist Wang | 10.1 | 89.9 | 100 | 10.35 | 19.65 | 30 | 70 |
| Assets: Dist Dual | 10.24 | 89.76 | 100 | 10.69 | 19.31 | 30 | 70 |
| Assets: Dist Tvar | 10.75 | 89.25 | 100 | 11.25 | 18.75 | 30 | 70 |
| Assets: Dist Blend | 11.98 | 88.02 | 100 | 11.62 | 18.38 | 30 | 70 |
Figure W
PIR Chapter 15, Figure 15.11, Loss and loss spectrums.
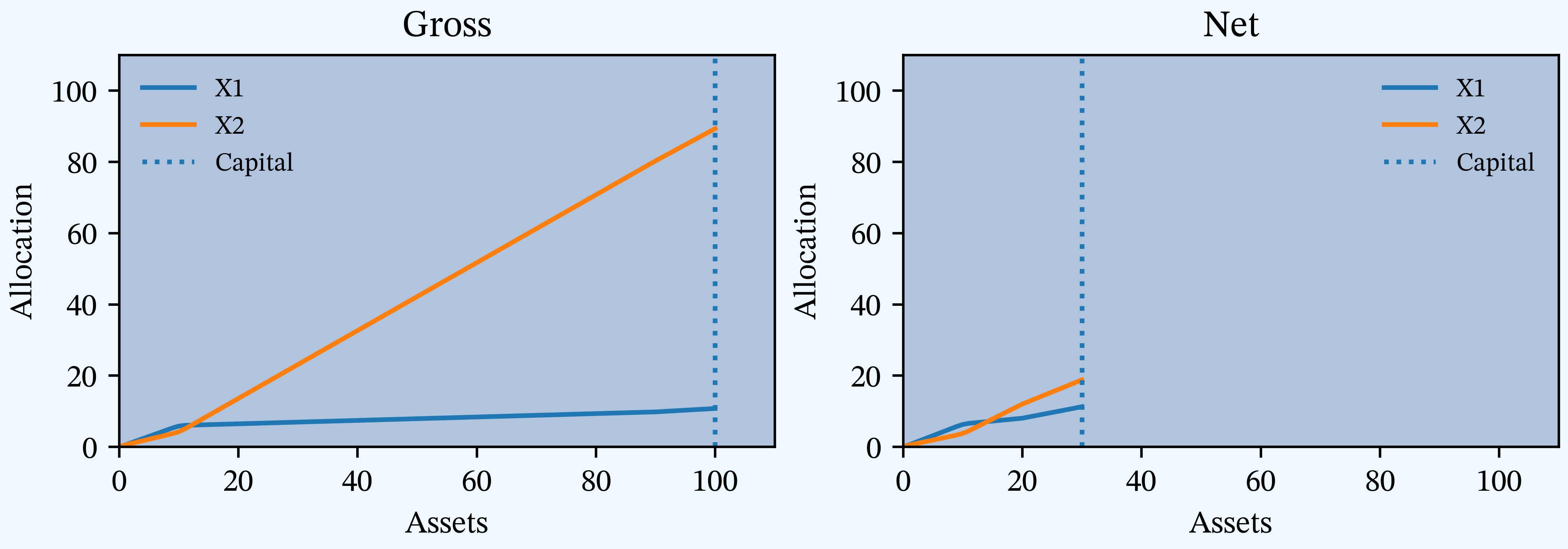
Figure X
PIR Chapter 15, Figures 15.12, 15.13, 15.14, Percentile layer of capital allocations by asset level.
Table Y
PIR Chapter 15, Tables 15.38, 15.39, 15.40, Percentile layer of capital allocations compared to distortion allocations.
| Method | Gross: X1 | Gross: X2 | Gross: Total | Net: X1 | Net: X2 | Net: Total | Ceded: Diff |
|---|---|---|---|---|---|---|---|
| Expected Loss | 17.27 | 82.73 | 100 | 14.25 | 15.75 | 30 | 70 |
| Dist Ccoc | 10 | 90 | 100 | 10 | 20 | 30 | 70 |
| Dist PH | 9.696 | 90.3 | 100 | 9.877 | 20.12 | 30 | 70 |
| Dist Wang | 10.1 | 89.9 | 100 | 10.35 | 19.65 | 30 | 70 |
| Dist Dual | 10.24 | 89.76 | 100 | 10.69 | 19.31 | 30 | 70 |
| Dist Tvar | 10.75 | 89.25 | 100 | 11.25 | 18.75 | 30 | 70 |
| Dist Blend | 11.98 | 88.02 | 100 | 11.62 | 18.38 | 30 | 70 |
| PLC | 10.75 | 89.25 | 100 | 11.25 | 18.75 | 30 | 70 |
Discrete (equal points) Case Description
PIR Discrete Case Study with equal points.
Distributions
# Line A (usually thinner tailed)
agg X1 1 claim dsev [0 9 10] [1/2 1/4 1/4] fixed
# Line B Gross (usually thicker tailed)
agg X2 1 claim dsev [0 1 90] [1/2 1/4 1/4] fixed
# Line B Net
agg X2 1 claim dsev [0 1 90] [1/2 1/4 1/4] fixed aggregate net of 70 xs 20Other Parameters
reg_p = 1roe = 0.1d2tc = 0.3s_values = [0.005, 0.01, 0.03]gs_values = [0.029126, 0.047619, 0.074074]f_discrete = Truelog2 = 8bs = 1padding = 1
Description of Tables and Figures
| Ref. | Kind | Chapter | Number(s) | Description |
|---|---|---|---|---|
| A | Table | 2 | 2.3, 2.5, 2.6, 2.7 | Estimated mean, CV, skewness and kurtosis by line and in total, gross and net. |
| B | Figure | 2 | 2.2, 2.4, 2.6 | Gross and net densities on a linear and log scale. |
| C | Figure | 2 | 2.3, 2.5, 2.7 | Bivariate densities: gross and net with gross sample. |
| D | Figure | 4 | 4.9, 4.10, 4.11, 4.12 | TVaR, and VaR for unlimited and limited variables, gross and net. |
| E | Table | 4 | 4.6, 4.7, 4.8 | Estimated VaR, TVaR, and EPD by line and in total, gross, and net. |
| F | Table | 7 | 7.2 | Pricing summary. |
| G | Table | 7 | 7.3 | Details of reinsurance. |
| H | Table | 9 | 9.2, 9.5, 9.8 | Classical pricing by method. |
| I | Table | 9 | 9.3, 9.6, 9.9 | Sum of parts (SoP) stand-alone vs. diversified classical pricing by method. |
| J | Table | 9 | 9.4, 9.7, 9.10 | Implied loss ratios from classical pricing by method. |
| K | Table | 9 | 9.11 | Comparison of stand-alone and sum of parts premium. |
| L | Table | 9 | 9.12, 9.13, 9.14 | Constant CoC pricing by unit for Case Study. |
| M | Figure | 11 | 11.2, 11.3, 11.4,11.5 | Distortion envelope for Case Study, gross. |
| N | Table | 11 | 11.5 | Parameters for the six SRMs and associated distortions. |
| O | Figure | 11 | 11.6, 11.7, 11.8 | Variation in insurance statistics for six distortions as \(s\) varies. |
| P | Figure | 11 | 11.9, 11.10, 11.11 | Variation in insurance statistics as the asset limit is varied. |
| Q | Table | 11 | 11.7, 11.8, 11.9 | Pricing by unit and distortion for Case Study. |
| R | Table | 13 | 13.1 missing | Comparison of gross expected losses by Case, catastrophe-prone lines. |
| S | Table | 13 | 13.2, 13.3, 13.4 | Constant 0.10 ROE pricing for Case Study, classical PCP methods. |
| T | Figure | 15 | 15.2 - 15.7 (G/N) | Twelve plot. |
| U | Figure | 15 | 15.8, 15.9, 15.10 | Capital density by layer. |
| V | Table | 15 | 15.35, 15.36, 15.37 | Constant 0.10 ROE pricing for Cat/Non-Cat Case Study, distortion, SRM methods. |
| W | Figure | 15 | 15.11 | Loss and loss spectrums. |
| X | Figure | 15 | 15.12, 15.13, 15.14 | Percentile layer of capital allocations by asset level. |
| Y | Table | 15 | 15.38, 15.39, 15.40 | Percentile layer of capital allocations compared to distortion allocations. |