Reinsurance Decision Making

A 20-Year Evolution

presentations
insurance
risk
pricing
What’s wrong the the constant cost of capital assumption
Author

Stephen J. Mildenhall

Published

2024-04-23

Abstract

“Reinsurance Decision Making: A 20-Year Evolution” challenges the constant cost of capital (aka risk-adjusted return on capital or RAROC) assumption commonly used in reinsurance evaluation and strategic insurance pricing—an assumption the weighted average cost of capital calculation reveals as invalid. The presentation demonstrates the advantages of using spectral pricing rules (SRMs), illustrating how SRMs not only generalize traditional methods like CoXTVaR but also address their limitations. Instead of prescribing a single solution, SRM methods offer a range of results corresponding to different risk appetites. A final section addresses the evaluation of reinsurance bought for reasons other than capital benefit, showing how reinsurance structured to maximize the continuous compounded net growth rate can simultaneously benefit the reinsurer and reinsured by recognizing the interconnectedness of past outcomes and future opportunities. An appendix provides technical details and references for practitioners to implement these methods on their own datasets.

The methods presented are applied to reinsurance evaluation but apply equally to setting profit targets and evaluating risk-adjusted returns by unit.

Contents

  1. Perspective
  2. Cost of Capital and Buyer Risk Appetite
  3. The Property Per Risk Conundrum
  4. Appendix

1. Perspective

Evolution 2003-2024

  • Old views

  • Issues and hidden assumptions

  • Updated views

Management Complaints and Refrains

  • Volatility vs. tail risk
  • “Balance”

Hidden Assumptions

  1. Cost of Capital (CoC) is constant
  1. Underwriter behavior is independent of reinsurance decisions
  1. You experience the average

2. CoC and Buyer Risk Appetite

Portfolio Pricing

In order to make insurance a trade at all, the common premium must be sufficient to compensate the common losses, to pay the expense of management, and to afford such a profit as might have been drawn from an equal capital employed in any common trade.”

 Adam Smith, Book 1, Ch X, Part I, 5th Edition, 1789

Portfolio Pricing

Adam Smith’s pricing rule

  • Portfolio pricing rule \[\mathrm{Premium} = \mathrm{common\ loss} + \mathrm{cost\ of\ capital}\]

  • Cost of capital, expressed in dollars averages, reflects

    • different forms of capital: equity, debt, reinsurance;
    • each with different cost rates

  • Excluding expenses, investment income (discount)

  • Distinguish capital from equity

  • Margin vs return and leverage

CoC Assumptions

Constant CoC assumption

  • Constant cost of capital (CCoC) is a standard assumption, ignoring alternatives

    • Vary across lines of business (too hard)
    • Vary across layers of capital (debt, equity, reinsurance, etc.)

  • CCoC of capital \(r\) is called target return on capital, WACC, opportunity cost of capital

  • CCoC pricing rule

    Premium = expected loss + \(r\) × (amount of capital)

CoC Assumptions

We know that CoC is not constant

  • That’s why we calculate WACC!
  • Debt credit curve
    • Higher rated debt (lower probability of default) is cheaper (lower yield)
    • Lower risk to the investor usually corresponds to a higher risk outcome for insurer (top of capital tower)
  • \(r\) × (amount of capital) = (Avg cost) x (Avg amount)
  • Generally, (Avg cost) x (Avg amount) \(\not=\) Avg(cost x amount)
  • Compare correlation: \(\mathsf E[XY]\not=\mathsf E[X]\mathsf E[Y]\)
  • Cat risk uses a lot of cheap capital \(\implies\) cost and amount negatively correlated
  • CCoC will overstate cost of cat risk: “too tail-centric”

Mathematics of CCoC

“The [reinsurance broker analyst] must understand symbols and speak in words.” John Maynard Keynes

“The [reinsurance broker analyst] must understand symbols and speak in words.” John Maynard Keynes

CCCoC pricing rule

For premium \(P\), expected loss \(\mathrm{EL}\), capital \(Q\), assets \(a\), and cost of capital \(r\)

  • \(P=\mathrm{EL} + r\,Q\)
  • \(\phantom{P}= \mathrm{EL} + r\,(a-P)\)
  • \(\phantom{P}= \displaystyle\frac{1}{1+r}\,\mathrm{EL} + \displaystyle\frac{r}{1+r}\,a\)
  • \(\phantom{P}= v\,\mathrm{EL} + d\,\max(\mathrm{loss})\)

using \(v\) and \(d\) for risk discount factor and rate of discount, \(v+d=1\), \(d=rv\)

CCoC Pricing Rule Implications

CCoC pricing rule has strange formulation

Premium = 0.87 x EL + 0.13 x max loss

for a 15% target return, \(v=1/1.15 = 0.87\) and \(d=0.13\)

Interpretation

  • Re-weighting of scenarios or probabilities?
    • Outcome x (Adjustment x Probability) not (Outcome x Adjustment) x Probability
    • 0.87 x EL: weight all scenario (probabilities) by factor of 0.87
    • Increase worst possible outcome probability to 0.13
  • Just math(s) reflecting CCoC pricing rule

CCoC Pricing Implications

  • Left plot shows CCoC risk (probability) adjustment factor distortion function relative to base at 1 (dashed line)
  • All outcome probabilities except the largest (“100%-percentile”) discounted by 0.87
  • Largest outcome probability increased to 0.13 (red star)
  • Right plot shows example total loss outcome as a quantile plot
  • Low (good) loss outcomes shown on left
  • High (bad) loss outcomes shown on right

Alternatives?

Re-weight using risk-adjusted probabilities

Imagine spreadsheet of equally likely scenarios. Want to re-weight with risk-adjusted probabilities. What properties must rational adjusted probabilities possess?

  1. Non-negative

  2. Sum to 1

  3. Increase with increasing loss

All bad outcomes that occur at a lower losses also occur for any larger loss

Risk-Adjusted Probabilities Reflecting “Volatility Aversion”

Meaning of volatility

  • Earnings miss

  • Plan miss

  • Bonus miss

Concern with outcomes near the mean

  • Solution: Apply maximal weight, consistent with (1)-(3) to a scenario at exceedance probability around 50%

Corresponding risk-adjusted probabilities

  • Result: Tail Value at Risk at \(p\) around 0.55

  • TVaR pricing: ignore best \(\approx 45\%\) of outcomes and average the rest

  • Comparison with usual XTVaR approach using \(p\approx 0.99\) presented in Appendix

Reflecting a Range of Risk Appetites

Five parametric families of distortion functions

  • CCoC \(\to\) PH (Proportional hazard) \(\to\) Wang \(\to\) dual \(\to\) TVaR
    • Five different one-parameter families of risk-adjusted probabilities
    • Each easily parameterized to desired pricing
    • Details in Appendix
  • Graph shows weight adjustments for comparably calibrated distortions

Distortion probability adjustment functions.

Distortion probability adjustment functions.
  • Dual distortion popular in client applications: bounded, weights all scenarios

Example: Cat Pricing Across a Range of Risk Appetites

Table 1: Assumptions for two-unit portfolio across 10 equally likely scenarios
  X1 X2 net X2 ceded X2 total
0 36 0 0 0 36
1 40 0 0 0 40
2 28 0 0 0 28
3 22 0 0 0 22
4 33 7 0 7 40
5 32 8 0 8 40
6 31 9 0 9 40
7 45 10 0 10 55
8 25 40 0 40 65
9 25 40 35 75 100
EX 31.7 11.4 3.5 14.9 46.6
CV 0.2149 1.299 3 1.545 0.4551
  • Unit X1 is non-cat
  • Unit X2 is cat exposed, shown split into net and ceded to 35 xs 40 cover

Example: Cat Pricing Across a Range of Risk Appetites

Pricing and loss ratios implied by dual distortion

Table 2: Expected loss, premium, and loss ratio by line
  L P LR
unit      
X1 31.7 32.31 0.9811
X2 14.9 21.26 0.701
X2 ceded 3.5 5.415 0.6464
X2 net 11.4 15.84 0.7196
total 46.6 53.57 0.87
  • Gross pricing at 87% loss ratio calibrated to 15% return with assets \(a=100\) sufficient to pay all claims, no-default
  • Loss ratio for X2 ceded loss represents model minimum acceptable ceded loss ratio

Example: Cat Pricing Across a Range of Risk Appetites

Pricing and loss ratios implied by dual distortion (details)

Table 3: Expected loss, premium, margin, capital, assets, loss ratio, leverage (PQ), and cost of capital by line
  L P M Q a LR PQ COC
unit                
X1 31.7 32.31 0.6096 13.83 46.14 0.9811 2.337 0.04409
X2 14.9 21.26 6.356 32.61 53.86 0.701 0.6518 0.1949
X2 ceded 3.5 5.415 1.915 13.12 18.54 0.6464 0.4125 0.1459
X2 net 11.4 15.84 4.441 19.48 35.32 0.7196 0.813 0.2279
total 46.6 53.57 6.965 46.43 100 0.87 1.154 0.15
  • Displays additive natural allocation of capital and associated average cost by unit; reflects lower capital cost for tail cat risk (see PIR Ch. 14.3.8)
  • Very low cost of capital for X1 reflects its value as a hedge; negative tail correlation

Example: Cat Pricing Across a Range of Risk Appetites

Model loss ratios across risk appetites

Table 4: Model loss ratios by distortion
unit X1 X2 net X2 ceded total
distortion        
ccoc 102.8% 75.3% 46.0% 87.0%
ph 101.7% 72.5% 52.5% 87.0%
wang 100.1% 72.1% 57.5% 87.0%
dual 98.1% 72.0% 64.6% 87.0%
tvar 95.7% 72.9% 72.9% 87.0%
  • All risk appetites calibrated to same total loss ratio
  • Distortions shown from tail-centric to volatility-centric
  • Ceded loss ratios show decreasing value of tail-reinsurance as risk appetite becomes more volatility driven
  • Conversely X1 loss ratio increases as tail-hedge becomes more valuable

Example: Cat Pricing Across a Range of Risk Appetites

CoC by unit across risk appetites

Table 5: Model natural allocation CoC by distortion
unit X1 X2 net X2 ceded total
distortion        
ccoc 15.0% 15.0% 15.0% 15.0%
ph -8.9% 18.9% 18.0% 15.0%
wang -0.3% 22.4% 18.3% 15.0%
dual 4.4% 22.8% 14.6% 15.0%
tvar 10.0% 22.0% 10.1% 15.0%
  • CCoC distortion results in constant CoC but perverse negative allocation to X1
  • CoC hard to interpret without CCoC assumption; better to work directly with margins
  • Interpret margin as the CFO’s cost to “enter the theme park” and expose all capital

Example: Cat Pricing Across a Range of Risk Appetites

Ceded CoC for reinsurance and equity capital

Table 6: Model indicated ceded CoC for equity and reinsurance capital
  Reins Equity Capital
distortion      
ccoc 15.0% 15.0% 15.0%
ph 11.2% 21.0% 15.0%
wang 8.9% 25.0% 15.0%
dual 6.5% 30.0% 15.0%
tvar 4.3% 34.9% 15.0%
  • Gross calibrated to 15% average return, determined by market dynamics
  • Purchase reinsurance when ceded ROE at or below indicated return
  • Reflects lower value ascribed to reinsurance by volatility-sensitive management

3: The Property Per Risk (PPR) Conundrum

Setup

  • Working layer casualty and property per risk often model with minimal benefit to diversified capital

  • Ceded ROE framework recommends against purchase

  • Recommendation predicated on hidden assumptions

    • CCoC
    • No change in uw behavior
    • No change in total cost of capital without underlying covers

  • Hidden assumptions questionable

    • UW may be risk averse (to call from angry CEO) or may lose discipline (“Make it up with diversification”)
    • Volatility may decrease size of allowable debt tranches and increase total cost of capital

Win/Win Reinsurance

Win/Lose

  • Cede above 100% loss ratio

  • Cede at higher than gross combined

  • Cedent and reinsurer cannot both win at once

  • Information / broking games?

  • Drives extreme cost focus

Win/Win?

  • Cedent objective: growth

  • Reality: bad year has implications for compounded growth

  • “Be there when the market turns”

  • Estimate expected compounded growth rate rather than growth rate at expected outcome

  • Opens possibility of win/win reinsurance

Example

Loss outcomes for simple illustrative example

Table 7: Simple property per risk model scenarios
  Probability Gross Ceded Net
Outcome        
Great 0.1 0 0 0
Average 0.8 1 0 1
Terrible 0.1 2 1 1
  • Simple setup: three outcomes easy to replicate in spreadsheet
  • Starting surplus 1, driven by premium leverage constraint
  • Probability of terrible outcome a parameter, EL calibrated to 1

Example: Pricing

Table 8: Expected loss, loss ratio, premium, and margin assumptions
  Gross Ceded Net
Item      
EL 1.000 0.100 0.900
LR 0.850 0.568 0.900
Premium 1.176 0.176 1.000
Margin 0.176 0.076 0.100
  • Pricing selected with broadly realistic gross and ceded loss ratios

Example: Return at Expected Outcome vs. Expected Return

  • Starting capital 1 in each case
  • Expected return measures expected continuously compounded return, \(\mathsf E[\log(X_1 / X_0)]\)
  • Underwriters locked into prior year results see returns over time for one scenario, not across scenarios
  • Premium volume linkage between years lowers average returns: an investment 20% up followed by 20% down, ends 4% down overall (\(0.8\times 1.2 = 24/25\))
Table 9: Return at expected outcome vs. expected returns
  Gross Net
Item    
Return @ expected 0.176 0.100
Expected return 0.034 0.070

Example: Implied Minimum Ceded Loss Ratios

Table 10: Benchmark ceded loss ratio that equates net and gross growth rates. A “buy” is indicated at this loss ratio or higher.
Prob risk loss 1.0e-06 1.0e-04 0.1% 1.0% 10.0% 25.0%
Gross LR            
75% 54.10% 54.10% 54.12% 54.24% 55.53% 57.63%
80% 49.71% 49.71% 49.72% 49.89% 51.51% 54.24%
85% 44.80% 44.81% 44.83% 45.02% 47.03% 50.48%
90% 39.09% 39.09% 39.11% 39.35% 41.80% 46.14%
95% 31.71% 31.71% 31.74% 32.03% 35.04% 40.59%
  • Counter-cyclical: more likely to purchase reinsurance as gross book profit declines
  • More likely to purchase reinsurance as terrible event probability declines—even below capital threshold
  • Other frameworks offer less responsive benchmarks and disappearing benefit for low probability outcomes

Example: Comparison with Spectral Approach

Method

  • Calibrate distortions to gross pricing with assets sufficient to pay all claims

  • Calculate natural allocation of gross premium to ceded and net

  • Compare loss ratios

Results

  • Spectral results less stable / usable

  • See details on next slide

  • ASOP 56: a model must be appropriate to the intended purpose

Example: Comparison with Spectral Approach

Table 11: 85% gross loss ratio, 10% chance terrible outcome
unit Ceded Net total
distortion      
ccoc 38.6% 98.1% 85.0%
ph 41.7% 96.1% 85.0%
wang 46.6% 93.6% 85.0%
dual 53.4% 91.0% 85.0%
tvar 56.7% 90.0% 85.0%
  • Growth-based ceded benchmark 47%
  • Between Wang and dual distortion
Table 12: 75% gross loss ratio, 10% chance terrible outcome
unit Ceded Net total
distortion      
ccoc 25.0% 96.4% 75.0%
ph 26.5% 94.1% 75.0%
wang 28.7% 91.4% 75.0%
dual 30.0% 90.0% 75.0%
tvar 30.0% 90.0% 75.0%
  • Growth-based ceded benchmark 55.5%
  • Opposite conclusion: spectral analysis more likely to buy reinsurance on more profitable book
Table 13: 85% gross loss ratio, 1% chance terrible outcome
unit Ceded Net total
distortion      
ccoc 5.4% 99.8% 85.0%
ph 5.5% 99.4% 85.0%
wang 5.7% 99.0% 85.0%
dual 5.7% 99.0% 85.0%
tvar 5.7% 99.0% 85.0%
  • Growth-based ceded benchmark 45%
  • Same conclusion: more likely to buy reinsurance on less likely tail event
  • But extreme reaction: buy reinsurance at almost any price (minimum ROLs)

4. Appendix

Spectral (SRM) Pricing

  • SRM pricing uses a distortion function to add a risk load

  • Distortion functions make bad outcomes more likely and good ones less, resulting in a positive loading

  • Distortions express a risk appetite

  • Portfolio SRM premium has a natural allocation to individual units

  • Many existing methods, including CoXTVaR, are special cases of SRMs

  • Different distortions can produce same total portfolio pricing but have materially different natural allocations to units, reflecting distinct risk appetites

  • Different allocations, in turn, drive materially different business decisions

Spectral (SRM) Pricing

  • Distortion function \(g\) maps a probability to a larger probability, used to fatten the tail

    • Increasing
    • Concave (decreasing derivative)

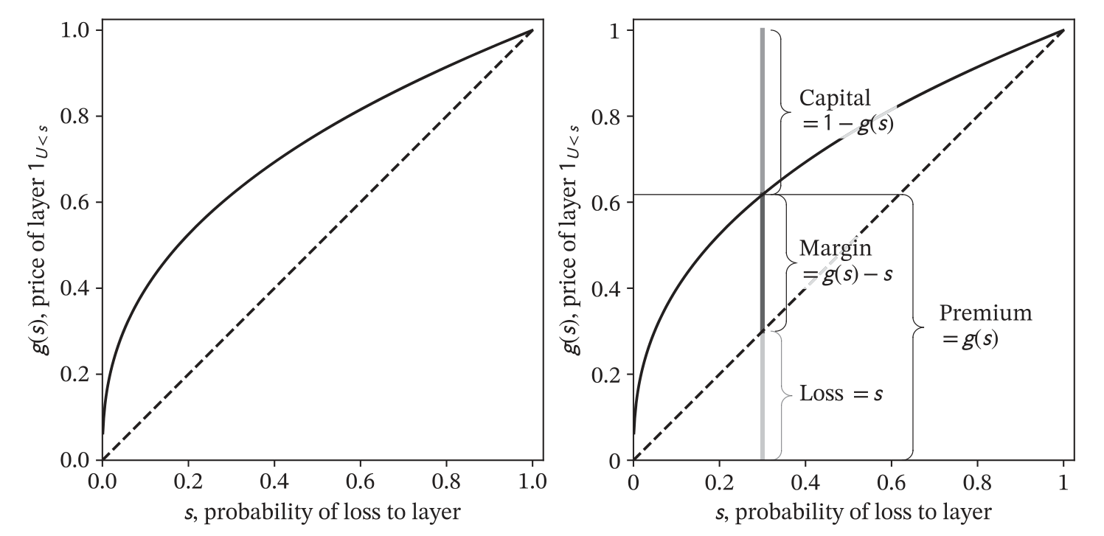
  • \(g(s)\) can be interpreted as the (ask) price to write a binary risk paying 1 with probability \(s\) and 0 otherwise

  • \(S(x) = \Pr(X>x)\), the survival function of a random variable \(X\) on sample space \(\Omega\)

    • Loss cost \(\mathsf E[X] =\displaystyle\int_\Omega S(x)dx\)

  • \(g(S(x)) > S(x)\) is the risk-adjusted survival function

Spectral Pricing

  • Spectral pricing rule associated with a distortion \(g\) is given by \[\rho(X) = \int_\Omega g(S(x))dx\] It is intrepreted as a price, technical premium, risk-adjusted loss cost, or risk measure

  • Integration by parts trick gives an alternative expression

    \[\rho(X) = \int_\Omega x g'(S(x))f(x)dx = \mathsf E[Xg'(S(X))]\]

    which makes the spectral risk adjustment by \(g'(S(X))\) explicit

Distortion Functions and Insurance Statistics

Spectral Pricing Rules Have Nice Properties

  1. Monotone: Uniformly higher risk implies higher price

  2. Sub-additive: diversification decreases price

  3. Comonotonic additive: no credit when no diversification; if out-comes imply same event order, then prices add

  4. Law invariant: Price depends only on the distribution

All risk measures with these properties are SRM rules

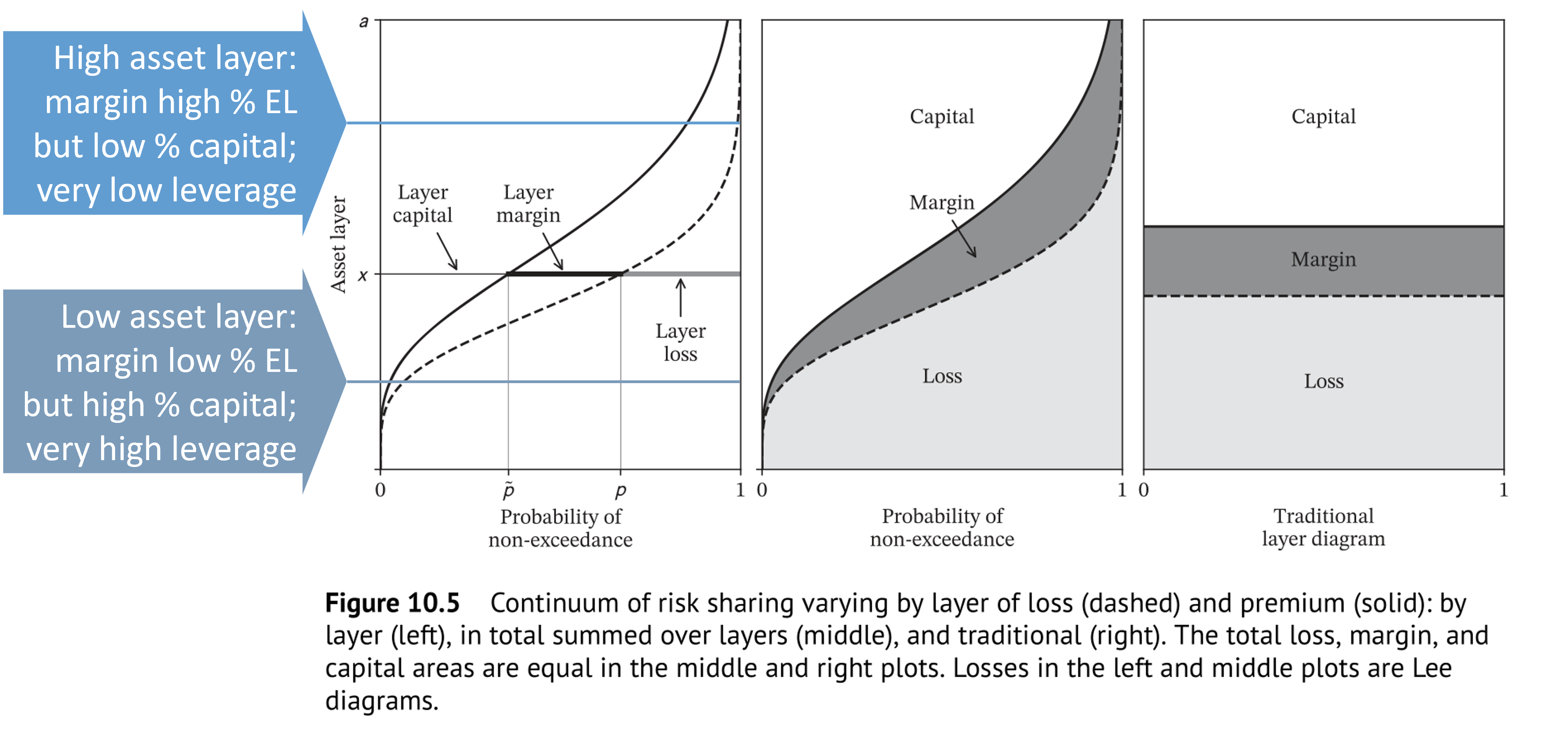
SRM Pricing Adds Up Pricing by Layer

SRM Pricing has a Natural Allocation to Sub-units

  • If \(X = \sum_i X_i\), define the natural allocation to unit \(i\) to be

\[\mathsf{NA}(X_i) = \mathsf E[X_i\, g'(S(X))]\]

  • Example: \(g(s)=\min(1, s / (1-p))\) corresponds to TVaR

    • \(\rho(X) =\mathsf{TVaR}_p(X)\)
    • \(\mathsf{NA}(X_i) = \mathsf{CoTVaR}_p(X_i)\)

  • The natural allocation pricing has nice properties

    • It is natural because it involves no additional assumptions
    • It adds-up because the sum of natural allocations is the original SRM price
    • It equals marginal pricing when marginal pricing is well defined

CCoC Portfolio Pricing

  • CCoC = constant cost of capital, a common but thoughtless and problematic default

    • Constant across layers of capital (debt, equity, etc.)
    • Know not to be true…when computing WACC!

  • Various names: target return on capital or WACC or cost of capital set equal to \(r\)

  • General portfolio pricing rule: Premium = expected loss + cost of capital

  • CCoC Portfolio pricing rule: Premium = expected loss + \(r\times\) (amount of capital)

CCoC Portfolio Pricing with XTVaR Capital Standard

  • CCoC implementation with XTVaR capital:

\[P(X) = \mathsf E[X] + r\, \mathsf{XTVaR}_p(X) = (1-r)\mathsf E[X] + r\, \mathsf{TVaR}_p(X)\]

  • Rule is a special case of SRM pricing

  • Corresponding distortion is \[g(s)=(1-r)s + r\min(1, s / (1-p))\]

    • Weight \(1-r\) applied to all events: risk neutral part
    • Weight \(r\) applied to \(p\)-tail events: extremely risk averse
    • Example of a bi-TVaR, an average of two TVaRs, since \(\mathsf E[X] = \mathsf{TVaR}_0(X)\)

  • Easy to check \(\rho(X) = (1-r)\mathsf E[X] + r\mathsf{TVaR}_p(X)\)

XTVaR Natural Allocation

  • Corresponding natural allocation is simply CoXTVaR pricing

\[\mathsf{NA}(X_i) = (1-r)\mathsf E[X_i] + r\, \mathsf{CoTVaR}(X_i) = \mathsf E[X_i] + r \, \mathsf{CoXTVaR}(X_i)\]

  • Shows SRM approach generalizes existing methods

  • Obvious question: What about using other distortions?

  • What does choice of distortion entail?

  • How can it be interpreted?

Distortions and Risk Appetite

Five “usual suspect” distortions

  • CCoC: \(g(s)=d + vs\) for \(s>0\) and \(g(0)=0\) where \(d=1/(1+r)\), \(v=1-d\) are discount rates

  • PH proportional hazard: \(g(s) = s^\alpha\), \(0 \le \alpha \le 1\)

  • Wang: \(g(s) = \Phi(\Phi^{-1}(s) +\lambda)\)

  • Dual: \(g(s) = 1 - (1 -s)^\beta\), \(\beta \ge 1\)

  • TVaR: \(g(s) = \min(1, s / (1-p))\)

Distortions and Risk Appetite

Calibrated distortion statistics for cat pricing example

Table 14: Distortion parameters for the two unit example from Section 2
  L P Q COC param error
method            
ccoc 46.6000 53.5652 46.4348 0.1500 0.1500 0.0000
ph 46.6000 53.5652 46.4348 0.1500 0.7205 0.0000
wang 46.6000 53.5652 46.4348 0.1500 0.3427 0.0000
dual 46.6000 53.5652 46.4348 0.1500 1.5952 -0.0000
tvar 46.6000 53.5652 46.4348 0.1500 0.2713 0.0000
  • Distortions easy to parameterize in Excel using Solver

Distortions and Risk Appetite

Calibrated distortion statistics for property risk example

Table 15: Distortion parameters for the PPR example base, 85% gross loss ratio and 10% chance terrible outcome
  L P Q COC param error
method            
ccoc 1.0000 1.1765 0.8235 0.2143 0.2143 0.0000
ph 1.0000 1.1765 0.8235 0.2143 0.6203 0.0000
wang 1.0000 1.1765 0.8235 0.2143 0.4911 0.0000
dual 1.0000 1.1765 0.8235 0.2143 1.9677 -0.0000
tvar 1.0000 1.1765 0.8235 0.2143 0.4334 0.0000
  • For all distortions except PH, a higher parameter produces higher prices; for PH lower parameter produces higher prices
  • These distortions are more expensive than the cat example

Algorithm for (Linear) Natural Allocation

  1. Compute unit average loss grouped by total loss & sum group probabilities
  2. Sort by ascending total loss (all values now distinct)
  3. Compute survival function S
  4. Apply distortion function g(S)
  5. Difference step 4 to compute risk adjusted probabilities Q
  6. Compute sum-products by unit and in total with respect to Q to obtain SRM pricing and natural allocation pricing by unit

Step 1 replaces \(X_i\) with the conditional expectation \(\mathsf E[X_i \mid X]\), a random variable defined by \(\mathsf E[X_i \mid X](\omega) = \mathsf E[X)i \mid X=X(ω)]\)

See PIR Algorithms 11.1.1 p.271 and 15.1.1, p.397 for more detail

See Why SRMs presentation for calculation details

Further Reading

Python source for presentation (RMarkdown) available on request

[1] for the theory of spectral risk measures, natural allocation, and implementation details

[2] for an introduction to the ideas behind the growth

[3] Modeling Standard of Practice for US Actuaries

References

1.
Mildenhall, S.J., Major, J.A.: Pricing insurance risk: Theory and practice. John Wiley & Sons, Inc. (2022)
2.
Peters, O.: Insurance as an ergodicity problem. Annals of Actuarial Science. 17, 215–218 (2023). https://doi.org/10.1017/S1748499523000131
3.
Actuarial Standards Board: Modeling. Actuarial Standard of Practice No. 56. (2019)