Particle Physics VSI

There are seventeen fundamental particles: six quarks, six leptons, and five bosons.

Main Page

Particle Physics

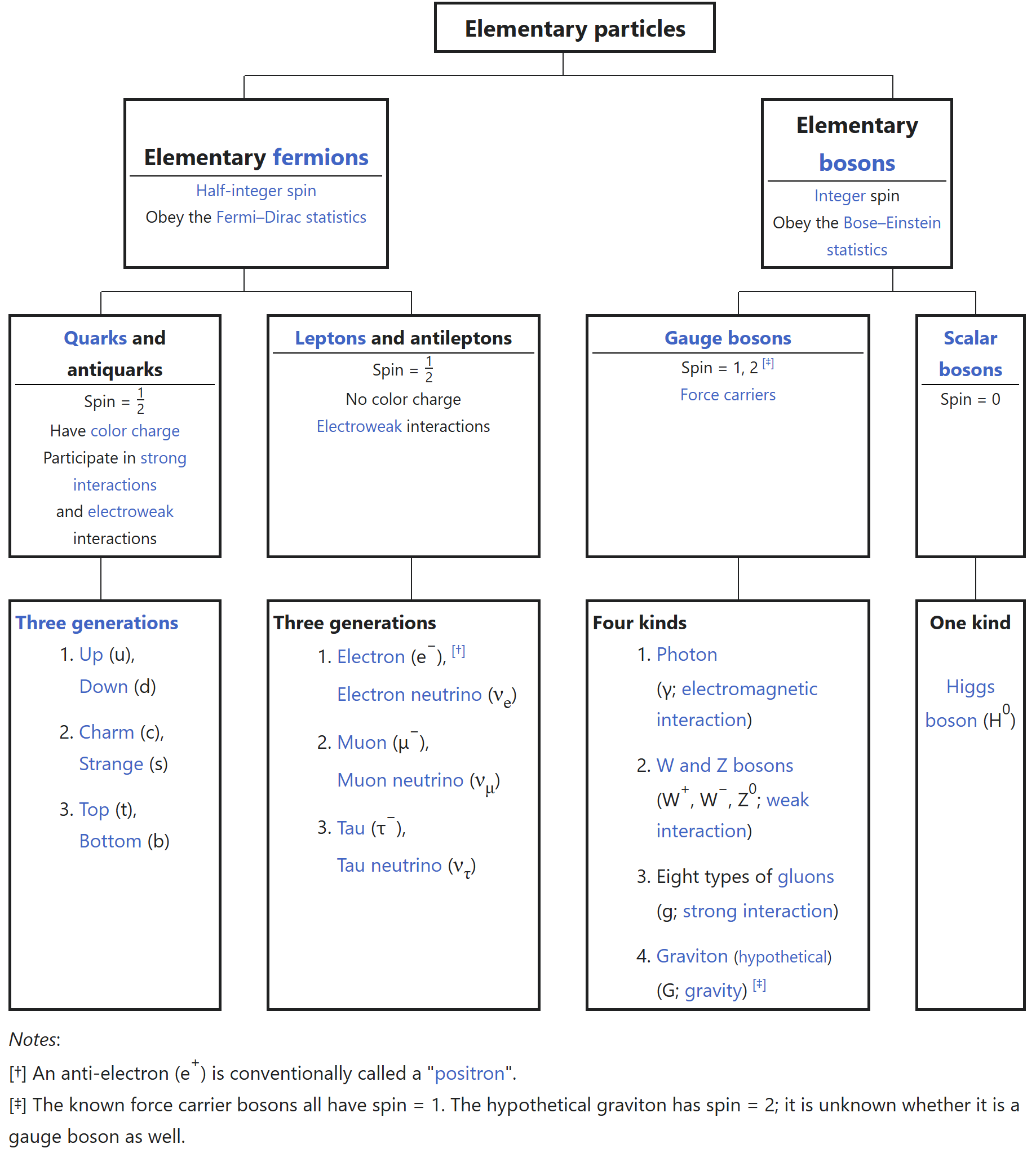
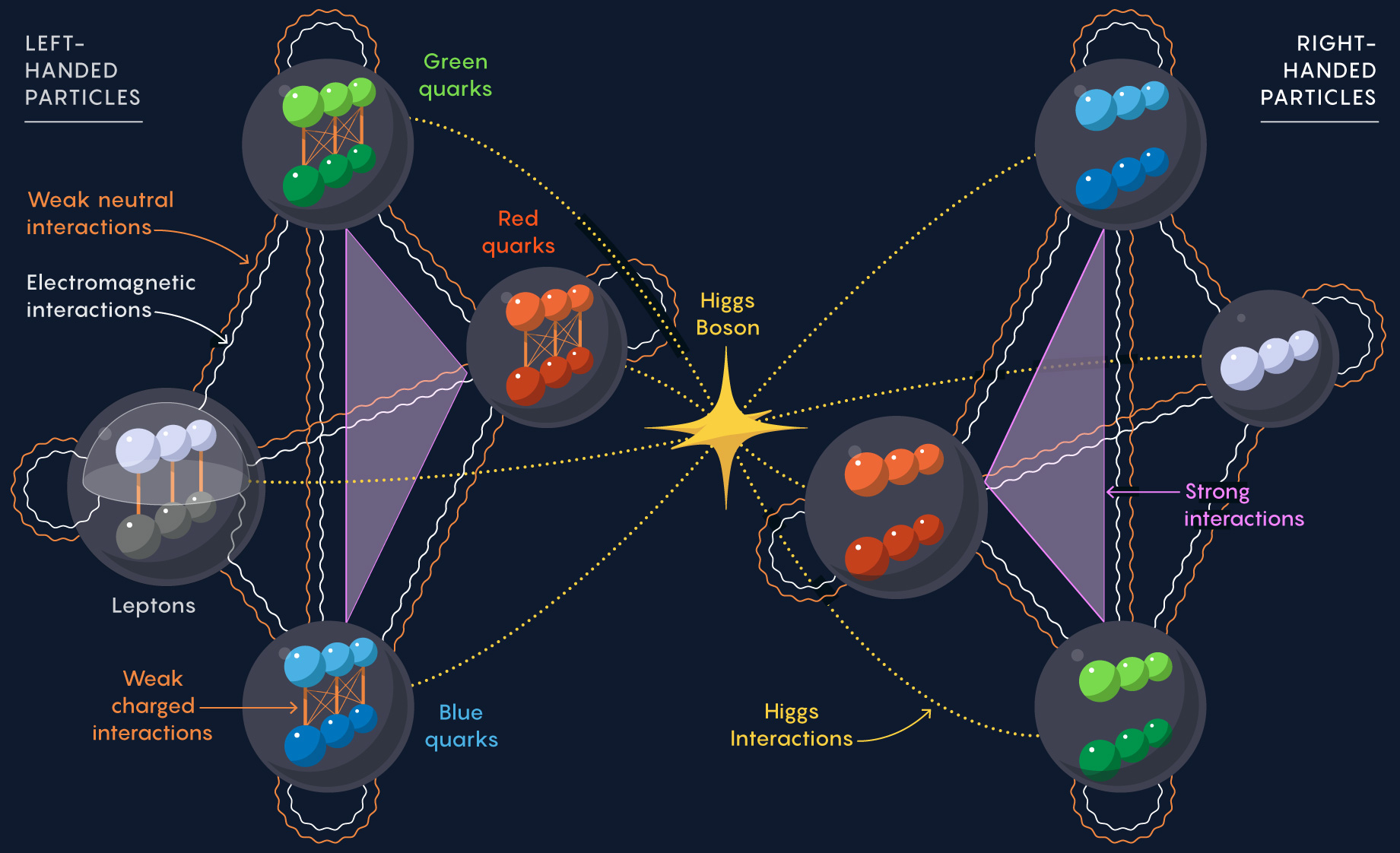
Seventeen Particles

There are seventeen fundamental particles (and corresponding antiparticles) comprising six quarks, six leptons, and five bosons. Fundamental and subatomic particles can be classified:

• Fermions obey Pauli exclusion principle
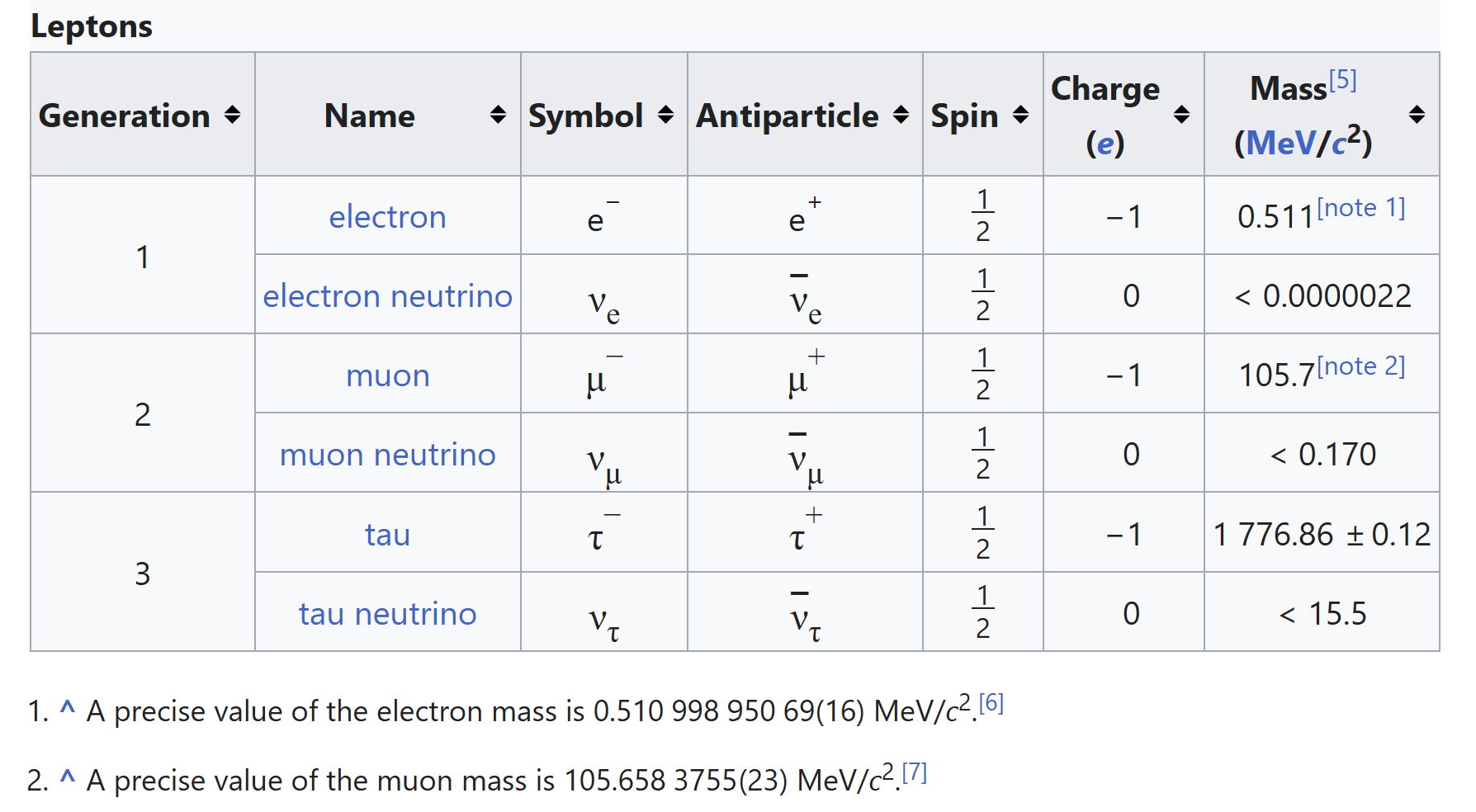
  • Leptons have no strong interaction: (\(e\), \(\mu\), \(\tau\), and neutrino versions)
  • Hadrons with strong interactions and are built from quarks
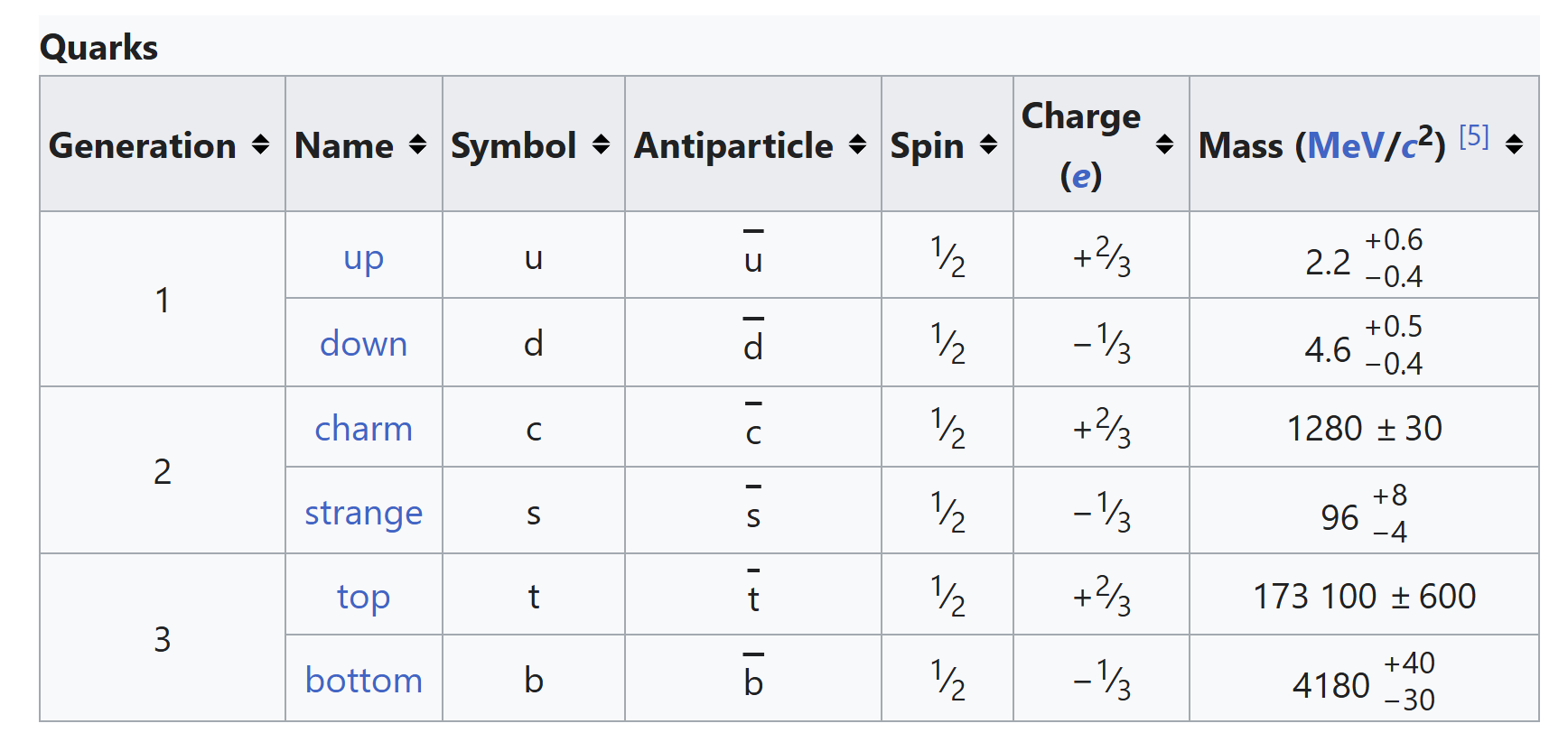
    • Quarks up/down, strange/charm, top/bottom; have color for strong interaction; quarks combine to form two sizes of hadron
      • Baryons made from three quarks; p, n, delta, sigma, xi, omega, charmed, bottom
      • Mesons made from two quarks; pion, kaons, eta
• Bosons no Pauli exclusion principle
  • Mediate forces between particles
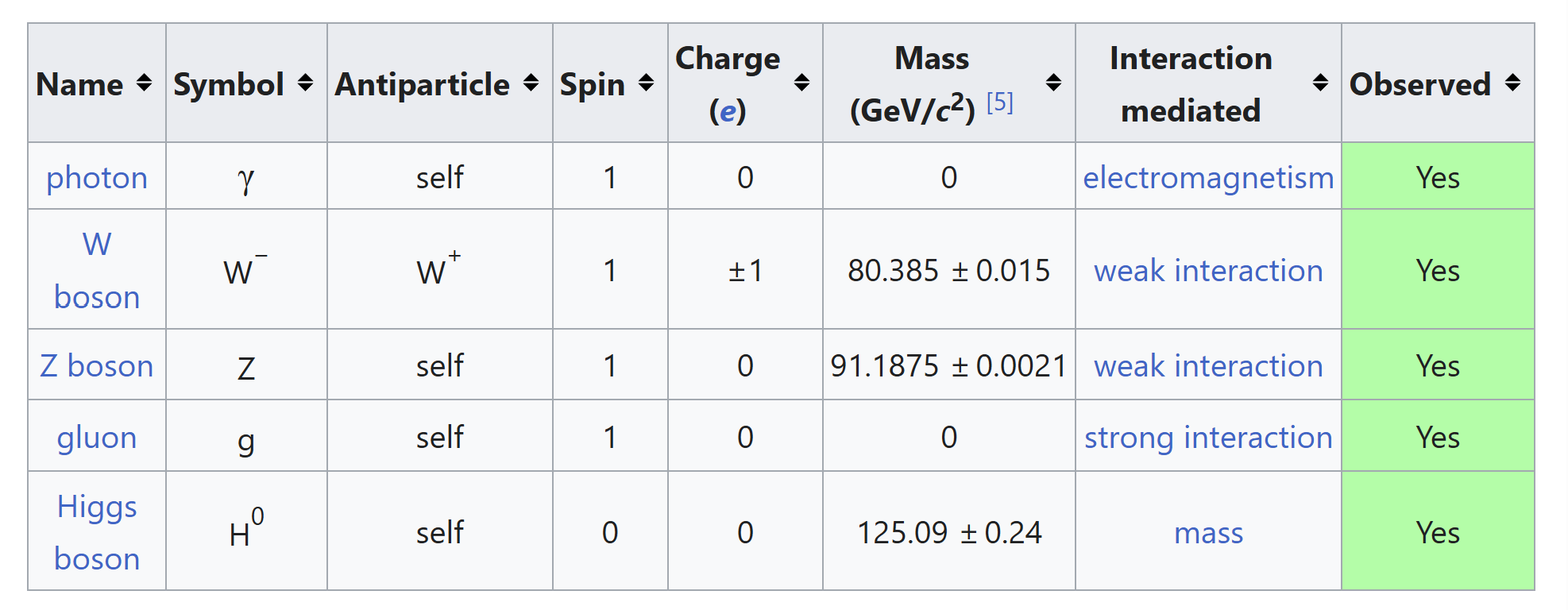
  • Gauge Bosons: \(g\), \(\gamma\), \(Z\), \(W\)
  • Scalar Boson: \(H\)

Useful Tables and Visualizations

Source: Elementary Particles on Wikipedia.

Flowchart of elementary particles.

Masses of elementary fermions.

Information about quarks.

Information about leptons.

Information about bosons.

Book Notes

• Energy, wavelength, temperature related: \(E=hc/\lambda = 10^{-6}/\lambda\)
• 1 eV = \(10^{-4} \times\) Kelvin temperature, energy gained by electron accelerated by 1 volt
• quark’s excited states are called resonances
• ionization removes electrons from an atom, but can’t break protons and neutron into separate quark constituents
• neutrinos are the commonest particles
• W is massive \(\rightarrow\) it is a short-range force
• 1 billion neutrinos were created in the universe per atom formed

Glossary

quark

seeds of protons, neutrons, and other hadrons

boson (after Satyendra Nath Bose)

integer spin, force carrier; photon, gluon (strong, joins quarks), W, Z (four gauge bosons), and Higgs (one scalar boson); do not obey Pauli exclusion principle

fermion (after Enrico Fermi)

half-integer spin, quarks and leptons; obeys Pauli exclusion principle; electron, p, n, neutrinos

lepton (“leptos” = small, fine)

do not feel strong force, half-integer spin; six types: electrons, muon, tau and their neutrinos

hadron (“hadros” meaning thick, heavy)

made of quarks and/or antiquarks and feels strong force

baryon (“barys” meaning heavy)

hadron made of three quarks; p (uud) or n (ddu); Delta, Sigma, Xi, Omega, Charmed, Bottom

meson (“mesos” meaning middle)

hadron made of a quark and anti-quark; pion, kaons, eta

color

property of quarks that is the source of the strong force

Representations of Particles

A New Map of All the Particles and Forces from Quanta Magazine includes the following.

Most common visualization.

Representation from 2013 film Particle Fever.

Three generations of quarks

• up / down
• charm / strange
• top / bottom

and electron \(\to\) muon \(\to\) tau, and neutrino flavors.

New map, three colors of quarks, three “sizes”.

GPT Notes

Fundamental Particles

Here is a table of fundamental particles, including quarks, leptons, and gauge bosons, along with their main properties:

Particle	Type	Symbol	Charge (e)	Mass (MeV/c²)	Spin	Interaction
Quarks
Up	Quark	u	+2/3	2.3	1/2	Strong, Weak, EM
Down	Quark	d	-1/3	4.8	1/2	Strong, Weak, EM
Charm	Quark	c	+2/3	1275	1/2	Strong, Weak, EM
Strange	Quark	s	-1/3	95	1/2	Strong, Weak, EM
Top	Quark	t	+2/3	173,000	1/2	Strong, Weak, EM
Bottom	Quark	b	-1/3	4180	1/2	Strong, Weak, EM
Leptons
Electron	Lepton	e⁻	-1	0.511	1/2	Weak, EM
Electron Neutrino	Lepton	νₑ	0	<0.0000022	1/2	Weak
Muon	Lepton	μ⁻	-1	105.7	1/2	Weak, EM
Muon Neutrino	Lepton	ν_μ	0	<0.17	1/2	Weak
Tau	Lepton	τ⁻	-1	1776	1/2	Weak, EM
Tau Neutrino	Lepton	ν_τ	0	<18.2	1/2	Weak
Bosons
Photon	Gauge Boson	γ	0	0	1	EM
W Boson	Gauge Boson	W⁺/W⁻	±1	80,379	1	Weak
Z Boson	Gauge Boson	Z⁰	0	91,188	1	Weak
Gluon	Gauge Boson	g	0	0	1	Strong
Higgs Boson	Scalar Boson	H	0	125,100	0	Scalar field

Explanation of Properties:

• Type: Classifies the particle as either a quark, lepton, or boson.
• Symbol: The common symbol used to represent the particle.
• Charge: The electric charge of the particle in units of elementary charge \(e\). Quarks have fractional charges, while leptons and bosons have integer charges or are neutral.
• Mass: The mass of the particle in MeV/c² (where MeV is mega-electron volts and \(c\) is the speed of light). Some particles, like neutrinos and gluons, have very small or effectively zero mass.
• Spin: A quantum property representing intrinsic angular momentum. Fermions (quarks and leptons) have half-integer spin (1/2), while bosons have integer spin (0 or 1).
• Interaction: The fundamental forces with which the particle interacts. These include the strong (affecting quarks and gluons), weak (affecting all fermions), electromagnetic (affecting charged particles), and scalar fields (affecting particles through the Higgs mechanism).

Temperature Since the Big Bang

Time Since Big Bang	Temperature (K)	Temperature (eV)	Constituents of the Universe	Additional Details
\(10^{-43}\) seconds	\(10^{32}\) K	\(8.617 \times 10^{27}\) eV	Quarks, leptons, photons, Higgs bosons	Planck era, quantum gravity effects dominate
\(10^{-35}\) seconds	\(10^{27}\) K	\(8.617 \times 10^{22}\) eV	Quarks, gluons, leptons, photons	Grand unification epoch, inflation starts
\(10^{-10}\) seconds	\(10^{15}\) K	\(8.617 \times 10^{10}\) eV	Quarks, gluons, W/Z bosons, Higgs bosons	Electroweak epoch, electroweak symmetry breaking
\(10^{-6}\) seconds	\(10^{13}\) K	\(8.617 \times 10^{8}\) eV	Quarks, gluons, leptons, photons	Quark-gluon plasma, hadronization begins
\(1\) second	\(10^{10}\) K	\(8.617 \times 10^{5}\) eV	Neutrons, protons, electrons, neutrinos, photons	Primordial nucleosynthesis starts
\(3\) minutes	\(10^{9}\) K	\(8.617 \times 10^{4}\) eV	Protons, neutrons, electrons, photons	Nucleosynthesis produces light elements (H, He, Li)
\(380,000\) years	\(3000\) K	\(0.26\) eV	Hydrogen, helium nuclei, electrons, photons	Recombination, CMB radiation emitted
\(1\) billion years	\(20\) K	\(1.7 \times 10^{-3}\) eV	Neutral atoms, dark matter, photons	Formation of first stars and galaxies
\(13.8\) billion years	\(2.725\) K	\(2.35 \times 10^{-4}\) eV	Neutral atoms, dark matter, dark energy, photons	Present-day universe

Energy and Wavelengths

Very short wavelengths correspond to high energy and temperature because they are concentrated in a very small area. This relationship can be understood through several principles in physics:

Wave-Particle Duality:

• Photon Energy: The energy of a photon is directly proportional to its frequency (\(\nu\)) and inversely proportional to its wavelength (\(\lambda\)): \[ E = h \nu = \frac{hc}{\lambda} \] where \(E\) is energy, \(h\) is Planck’s constant, \(c\) is the speed of light, \(\nu\) is frequency, and \(\lambda\) is wavelength.
• Short Wavelength, High Energy: As the wavelength decreases (becomes shorter), the frequency increases, leading to higher energy photons.

Temperature and Radiation:

• Blackbody Radiation: The temperature of an object is related to the spectrum of electromagnetic radiation it emits. According to Wien’s displacement law, the peak wavelength (\(\lambda_{\text{max}}\)) of the emitted radiation is inversely proportional to the temperature (\(T\)): \[ \lambda_{\text{max}} T = b \] where \(b\) is Wien’s displacement constant.
• High Temperature, Short Wavelength: Higher temperatures correspond to shorter peak wavelengths of emitted radiation, indicating higher energy photons.

Energy Concentration:

• Energy Density: High-energy photons with short wavelengths can be thought of as having their energy concentrated in a small spatial region, leading to high energy density.
• Quantum Effects: At very short wavelengths (high frequencies), quantum effects become significant, allowing the creation of particle-antiparticle pairs when the energy is high enough.

Summary:

• Short Wavelengths, High Energy: Short wavelengths are associated with high energy because the photon’s energy is inversely proportional to its wavelength.
• High Temperature, High Energy: High temperatures lead to the emission of higher energy photons with shorter wavelengths.
• Energy Concentration: Short wavelengths imply that the energy is confined to a small spatial region, resulting in high energy density, which is consistent with high temperatures.

Table

The next table shows the corresponding speeds (as a fraction of the speed of light \(c\)) for electrons and protons to generate the given energy levels. This can be derived using the relativistic kinetic energy formula: \[ E = \gamma m c^2 - m c^2 = (\gamma - 1) m c^2 \] where:

• \(E\) is the kinetic energy.
• \(\gamma\) is the Lorentz factor, \(\gamma = \frac{1}{\sqrt{1 - (v/c)^2}}\).
• \(m\) is the rest mass of the particle.
• \(v\) is the velocity of the particle.

For simplicity, we solve for \(v\) in terms of \(E\), \(m\), and \(c\).

Type of Radiation	Energy (eV)	Wavelength (m)	Temperature (K)	Particles Created	Speed of Electron (fraction of \(c\))	Speed of Proton (fraction of \(c\))
Radio Waves	\(10^{-6} - 10^{-3}\) eV	\(10^3 - 10^{-1}\) m	\(10^{-2} - 10\) K	None (thermal motion of atoms/molecules)	\(\approx 10^{-3}\) - \(10^{-1}\)	\(\approx 10^{-5}\) - \(10^{-3}\)
Microwaves	\(10^{-3} - 10^{-1}\) eV	\(10^{-1} - 10^{-3}\) m	\(10 - 10^2\) K	None (thermal motion of atoms/molecules)	\(\approx 10^{-1}\) - \(0.4\)	\(\approx 10^{-3}\) - \(10^{-2}\)
Infrared	\(10^{-1} - 1\) eV	\(10^{-3} - 7 \times 10^{-7}\) m	\(10^2 - 10^4\) K	None (thermal motion of atoms/molecules)	\(0.4\) - \(0.9\)	\(10^{-2}\) - \(0.03\)
Visible Light	\(1.65 - 3.1\) eV	\(7 \times 10^{-7} - 4 \times 10^{-7}\) m	\(4 \times 10^3 - 10^4\) K	None (excitation of electrons in atoms)	\(0.9\) - \(0.98\)	\(0.03\) - \(0.05\)
Ultraviolet	\(3.1 - 100\) eV	\(4 \times 10^{-7} - 10^{-8}\) m	\(10^4 - 10^6\) K	Excitation/ionization of electrons	\(0.98\) - \(0.999\)	\(0.05\) - \(0.3\)
X-Rays	\(100 - 10^5\) eV	\(10^{-8} - 10^{-11}\) m	\(10^6 - 10^9\) K	Ionization of atoms, creation of electron-positron pairs	\(0.999\) - \(0.99999\)	\(0.3\) - \(0.87\)
Gamma Rays	\(10^5 - 10^{12}\) eV	\(10^{-11} - 10^{-15}\) m	\(10^9 - 10^{12}\) K	Creation of electron-positron pairs, possible creation of heavier particles like muons at higher energies	\(0.99999\) - \(0.999999999\)	\(0.87\) - \(0.99999\)
High-Energy Gamma Rays	\(10^{12} - 10^{15}\) eV	\(10^{-15} - 10^{-18}\) m	\(10^{12} - 10^{15}\) K	Creation of muon pairs, pion pairs	\(\approx 0.999999999\)	\(0.99999\) - \(0.999999\)
Ultra-High-Energy Gamma Rays	\(10^{15} - 10^{19}\) eV	\(10^{-18} - 10^{-22}\) m	\(10^{15} - 10^{19}\) K	Creation of hadrons (protons, neutrons), mesons (pions, kaons)	\(\approx 0.9999999999\)	\(0.999999\) - \(0.999999999\)
Grand Unification Energy	\(10^{19}\) eV and above	\(< 10^{-22}\) m	\(> 10^{19}\) K	Creation of all known particles, potential formation of new particles like magnetic monopoles	\(\approx 1\)	\(\approx 1\)

Explanation:

• Speed of Electron/Proton (fraction of \(c\)): The speed is calculated for each energy level using relativistic formulas, showing how close the particle’s speed is to the speed of light. Electrons, being much lighter than protons, achieve higher fractions of \(c\) at lower energy levels compared to protons.

Large Hadron Collider

The Large Hadron Collider (LHC) is the world’s largest and most powerful particle accelerator, located at CERN (the European Organization for Nuclear Research) near Geneva, Switzerland. It was built to explore the fundamental properties of matter by colliding protons (and sometimes heavy ions) at unprecedented energies.

• Location: Near Geneva, Switzerland, straddling the French-Swiss border.
• Circumference: 27 kilometers (17 miles).
• Operational Since: 2008.
• Energy: Initially designed to reach collision energies of 14 TeV (tera-electron volts) in the center of mass frame, though initial operations have been at lower energies.

Major Discoveries:

1. Higgs Boson (2012):
   • Discovery Date: July 4, 2012.
   • Significance: The discovery of the Higgs boson was a monumental achievement in physics. It confirmed the existence of the Higgs field, which gives mass to elementary particles. This discovery provided key validation for the Standard Model of particle physics.
   • Experiments Involved: ATLAS and CMS (two of the main detectors at the LHC).
2. Observation of Exotic Hadrons:
   • Significance: The LHC has discovered several exotic hadrons, including tetraquarks and pentaquarks, which are combinations of four and five quarks, respectively. These findings provide deeper insights into the strong interaction and the behavior of quarks.
   • Examples:
     • Tetraquark \(Z_c(3900)\) discovered in 2013.
     • Pentaquark states \(P_c(4380)^+\) and \(P_c(4450)^+\) discovered in 2015.
3. Study of Quark-Gluon Plasma:
   • Significance: By colliding heavy ions, the LHC has created and studied quark-gluon plasma, a state of matter thought to have existed shortly after the Big Bang. This helps physicists understand the properties of the strong force and the early universe.
4. Measurement of Standard Model Parameters:
   • Significance: The LHC has provided precise measurements of Standard Model parameters, such as the mass of the top quark, the W and Z bosons, and various coupling constants. These measurements help test the consistency of the Standard Model.
5. Search for New Physics:
   • Significance: Although no direct evidence for new physics beyond the Standard Model has been found, the LHC continues to search for signs of supersymmetry, extra dimensions, and other theoretical extensions. The constraints and limits set by these searches are crucial for guiding future theoretical developments.

Future Prospects:

• High-Luminosity LHC (HL-LHC): Upgrades are underway to increase the luminosity (collision rate) of the LHC, allowing for more data collection and increasing the sensitivity to rare processes and new phenomena.
• Exploration of Higher Energies: Potential future upgrades or new accelerators aim to reach even higher energies, further probing the fundamental structure of matter and the universe.

The Large Hadron Collider has been instrumental in advancing our understanding of particle physics, with its most notable achievement being the discovery of the Higgs boson in 2012. It continues to provide valuable data, enhancing our knowledge of the Standard Model and searching for new physics phenomena.

Mass of Neutrinos

The exact masses of neutrinos are still not precisely known, but significant progress has been made in determining their properties. Here are the key points about neutrino masses:

1. Non-Zero Mass: It is established that neutrinos have a non-zero mass, contrary to the original assumption in the Standard Model that they are massless. This discovery came from observations of neutrino oscillations.

2. Neutrino Oscillations:

   • Neutrino oscillations are a phenomenon where neutrinos switch between different flavors (electron, muon, tau) as they travel. This can only happen if neutrinos have mass and the different mass states are not equal.
   • Experiments such as those conducted by Super-Kamiokande, SNO (Sudbury Neutrino Observatory), and others have provided strong evidence for neutrino oscillations.

3. Mass Differences:

   • While the absolute masses of the neutrinos are not known, the differences in the squares of the masses (mass squared differences) have been measured:
     • Solar Neutrinos: \(\Delta m_{21}^2 \approx 7.53 \times 10^{-5} \, \text{eV}^2\)
     • Atmospheric Neutrinos: \(\Delta m_{32}^2 \approx 2.44 \times 10^{-3} \, \text{eV}^2\)

4. Upper Limits:

   • Direct experiments such as the KATRIN (Karlsruhe Tritium Neutrino) experiment aim to measure the absolute mass of neutrinos. KATRIN has set an upper limit on the effective electron neutrino mass of about 0.8 eV.
   • Cosmological observations also provide constraints on the sum of neutrino masses, suggesting it is less than about 0.12 eV.

Neutrinos have non-zero masses, but their exact values remain unknown. Current research focuses on narrowing down these values through direct measurements and indirect constraints from oscillation experiments and cosmological data.

Higg’s Mechanism

The Higgs mechanism is a process by which particles acquire mass through their interaction with the Higgs field. This mechanism is a fundamental part of the Standard Model of particle physics and was proposed to explain how particles that should be massless (according to the symmetry of the theory) actually have mass.

Key Concepts:

1. Higgs Field:
   • A scalar field that permeates all of space.
   • Particles interact with this field to gain mass.
2. Higgs Boson:
   • The quantum excitation of the Higgs field.
   • Discovered in 2012 at the Large Hadron Collider (LHC).
3. Spontaneous Symmetry Breaking:
   • The Higgs field has a non-zero vacuum expectation value (VEV), meaning it has a constant value even in its lowest energy state.
   • This breaks the symmetry of the electroweak interaction, giving mass to the W and Z bosons while the photon remains massless.

How it Works:

• Particles interact with the Higgs field, and the strength of this interaction determines their mass.
• Particles like the W and Z bosons interact strongly with the Higgs field and thus gain significant mass.
• The Higgs boson itself is a manifestation of fluctuations in the Higgs field.

Mathematical Overview:

• The Lagrangian of the Standard Model includes a potential for the Higgs field \(V(\phi)\), typically having a form that allows for spontaneous symmetry breaking: \[ V(\phi) = \mu^2 \phi^\dagger \phi + \lambda (\phi^\dagger \phi)^2 \] where \(\phi\) is the Higgs field, \(\mu^2\) is a parameter that determines the shape of the potential, and \(\lambda\) is a coupling constant.

• The Higgs field acquires a non-zero value in the vacuum state: \[ \langle \phi \rangle = \frac{\mu}{\sqrt{\lambda}} \]

• This non-zero vacuum expectation value (VEV) leads to mass terms for the W and Z bosons and other particles in the Standard Model.

The discovery of the Higgs boson confirmed the existence of the Higgs field and the validity of the Higgs mechanism in explaining how particles acquire mass.

The Higgs field played a crucial role in the early universe, particularly during a phase known as electroweak symmetry breaking. Here’s a more detailed explanation:

Early Universe:

• Variable and Dynamic: Shortly after the Big Bang, the universe was in a highly energetic and hot state. During this time, the Higgs field was in a symmetric phase with a value of zero, meaning particles were massless.
• Electroweak Symmetry Breaking: As the universe expanded and cooled, it underwent a phase transition. The Higgs field acquired a non-zero vacuum expectation value (VEV), breaking the electroweak symmetry. This process gave mass to the W and Z bosons, as well as other particles interacting with the Higgs field, while the photon remained massless.

Present Universe:

• Settled State: Today, the Higgs field has settled into a stable, non-zero value throughout space. This value acts as a consistent background field.
• Consistent Background Force: The Higgs field now provides a constant mechanism through which particles acquire mass. It is no longer variable or dynamic in the way it was during the early universe but instead provides a uniform and stable background influence.

In summary, the Higgs field was more variable and played a dynamic role in the early universe, leading to the masses of fundamental particles. Today, it acts as a largely consistent background force, maintaining the masses of particles in a stable manner.

Higgs vs. Water Freezing

The phase transition of the Higgs field in the early universe is conceptually similar to the phase transition of water freezing into ice. Here’s a comparison to clarify the analogy:

Water to Ice Transition:

• Initial State: Water is in a liquid state at high temperatures.
• Cooling: As the temperature drops, the kinetic energy of water molecules decreases.
• Phase Transition: At 0°C, water molecules begin to arrange themselves into a crystalline structure, forming ice. This transition releases latent heat.
• Final State: Ice has a different structure and properties compared to liquid water.

Higgs Field Transition:

• Initial State: In the extremely hot early universe, the Higgs field is symmetric and has a value of zero, meaning particles are massless.
• Cooling: As the universe expands and cools, the energy conditions change.
• Phase Transition (Electroweak Symmetry Breaking): At a critical temperature, the Higgs field undergoes a phase transition, acquiring a non-zero vacuum expectation value (VEV). This breaks the electroweak symmetry, giving mass to particles like W and Z bosons.
• Final State: The Higgs field now has a non-zero value throughout space, providing a consistent mechanism for particles to have mass.

Key Similarities:

• Change in State: Both involve a change from one state to another (symmetric to broken symmetry for the Higgs field, liquid to solid for water).
• Critical Temperature: Both transitions occur at a specific temperature threshold.
• Latent Energy: Both transitions involve changes in energy distributions.

Key Differences:

• Nature of Transition: The Higgs field transition involves quantum fields and fundamental forces, whereas water to ice is a macroscopic physical change.
• Scale: The Higgs field transition occurred at a fundamental particle level in the early universe, whereas water to ice happens at a molecular level in everyday conditions.

In summary, while the phase transition of the Higgs field is much more complex and fundamental in nature, the analogy to water freezing into ice helps to illustrate the concept of a critical temperature leading to a change in state and properties.

Deets

• Frank Close
• Volume 109
• Published 2012 (revised with corrections)